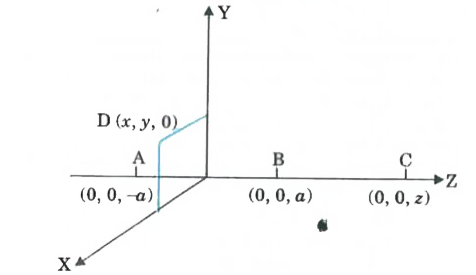
Two charges -q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ? (b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1.
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
(a) From the figure given below the potential due to the both the charges at point C (0, 0, z) can be calculated as:
V=q4πε0(z−a)+(−q)4πε0(z+a)=q(2a)4πε0(z2−a2)
Potential due to both the charges at point D (x, y, 0) will be zero as both the charges are at equal distance from this point.
(b) Potential at any point due to an electric dipole is represented as V=14πε0pcosθr2−a2cos2θ
(This result has been obtained in the sub-section: 2.3.4(c): Electric potential at a general location due to a short electric dipole)
For short electric dipole ra>>1
Or, r>>a
Thus, a2cos2θ can be neglected in comparisonto r2 in the denominator. Hence, we can write electric potential due to short electric dipole as:
V=14πε0pcosθr2⇒V∝1r2
(c ) As both the charges constituting electric dipole lie on Z-axis and points (5, 0, 0) and (-7, 0, 0) lies on (X-axis), it lies in the equatorial plane of the electric dipole. Thus, potential at both the points are zero and work done in moving a test charge from (5, 0, 0) to (-7, 0, 0) will be zero.
As electrostatic field is conservative in nature, thus the work done by it will be independent of path. Thus answer will remain same, even if the path of the test charge is changed.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Additional Exercises) (Answer carefully)
Explore 7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Additional Exercises) (Answer the following)
Explore 4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Textbook Exercise)
Explore 11 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Two charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
What is the electrostatic potential at the points (0, 0, z) and (x, y,0) ?
View SolutionTwo charges -q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ? (b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1.
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View Solution
Knowledge Check
Two point charges −q and +q are located at points (0,0−a) and (0,0,a) resepctively.The electric potential at point (0,0,z)is (Z>a)
Aqa4πε0z2Bq4πε0aC2qa4πε0(z2−a2)D2qa4πε0(z2+a2)Two point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
A2qd4πε0(d2+a2)3/2ˆkBqd4πε0(d2+a2)3/2ˆkC−2qd4πε0(d2+a2)3/2ˆkD−qd4πε0(d2+a2)3/2ˆk
Two charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
How much work is done in moving a small test charge from the point (5, 0, 0) to (-7,0,0) along the x-axis ? Does the answer change if the path of the test charge between the same points is not along the x-axis ?
View SolutionTwo charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
Obtain the dependence of potential on the distance r of a point from the origin when ra>>1.
View SolutionTwo charges - q and + q are located at points A(0, 0, -a) and B(0, 0, +a) respectively. How much work is done in moving a test charge from point P(7,0,0) to Q(-3,0,0) ?
View SolutionTwo point charges q and - q are located at points (0 , 0 , - a ) and (0 , 0 , a) respectively :
(a) Find the electrostatic potential at (0 , 0 , z) and ( x , y , 0).
(b) How much work is done in moving a small test charge from the point (5 , 0 , 0 , ) to (-7 , 0 , 0 ) along the x - axis ?
(c) How would your answer change if the path of the test charge between the same points is not along the x axis but along any other random path ?
(d) If the above point charges are now placed in the same position in a uniform external electric field →E, what would be the potential energy of the charge system in its orientation of unstable equilibrium ? Justify your answer in each case .
View Solution(i) Can two equpotential surfaces intersect each other ? Give reason.
(ii) Two charges +qand−q are located at points A (0,0,−2)andB(0,0,2) respectively. How much work will be done in moving a test charge from point P(4,0,0) to (−5,0,0) ?
View SolutionTwo charges −qand+q are located at points A(0,0,−a)andB(0,0+a). How much work is done in moving a test charge from point (b,0,0) to Q(−b,0,0) ?
View Solution

