A point charge +Q is place just outside an imaginary hemispherical surface of radius R as shown in the figure. Which of the following statements is/are correct ?
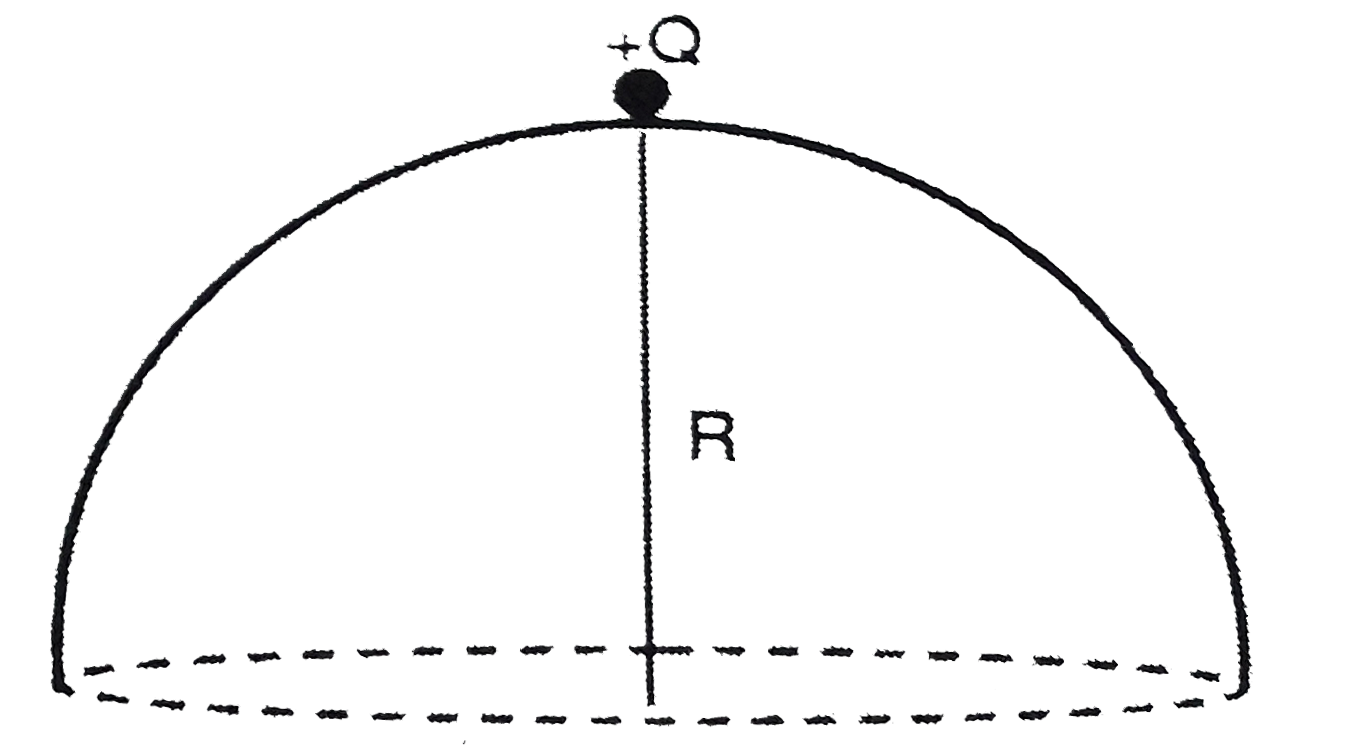
Total flux through the curved and the flat surface is Qε0
The component of the electric field normal to the flat surface is constant over the surface
The circumference of the flat surface in an equipotential
The electric flux party through the curved surface of the hemisphere is −Q2ε0(1−1√2)
The correct Answer is:C, D
Flux through a closed three dimensional surface is Q/ε0, where Q is enclosed charged within the 3D surface. Here charge is outside the given surface hence we need to extend the surface to enclose the charge. Hence flux through given surface has to be less than Q/ε0. Hence option (a) is wrong.
(b) Refer following figure.

E⊥=Ecosθ
When we move away from the centre, on flat circular face of hemisphere, then electric field intensity decreases due to increase in distance of the point from point charge. At the same time angle between electric field intensity and normal also increases. Hence component of electric field normal to the surface cannot be same for all points on circular face. Hence option (b) is wrong.
(c )Distance of any point on circumference of circular face from point charge is R√2. Hence there will be same potential for all points.
V=14πε0Q√2R
Hence option (c) is correct .
(d)Electric flux linked with curved surface is same as that with circular face of hemisphere, except that it is negative for curved surface whereas positive for the circular face. We can calculate flux for the circular face and then apply negative sign to write the flux for curved surface. Note that electric lines will enter the curved surface and the same will come out from flat circular face.
Solid angle made by circular face at the location of point charge can be written as follows:
Ω=2π(1−cosθ)
Here θ=45∘
Total solid angse around the charge is 4π hence flux associated with circular face can be written as follows (Proportional to solid angle)
ϕ=Ω4π×Qε0=−2π(1−cosθ)4πQε0
=Q2ε0(1−1√2)
Same negative flux is associated with curved surface hence option (d) is correct.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (D.MCQ) Passage )
Explore 10 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (Assertion Reason ) )
Explore 15 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (BC.MCQ))
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
Locate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:

View SolutionA charge q is situated at the centre of an imaginary hemispherical surface, as shown in figure. Using gauss's theorem and symmetry considerations, determine the electric flux due to this charge through the hemisphere surface.
View Solution
Knowledge Check
q1,q2,q3 and q4 are point charges located at point as shown in the figure and S is a spherical Gaussian surface of radius R. Which of the following is true according to the Gauss's law
 A∮s(→E1+→E2+→E3).d→A=q1+q2+q32ε0B∮s(→E1+→E2+→E3).d→A=(q1+q2+q3)ε0C∮s(→E1+→E2+→E3).d→A=(q1+q2+q3+q4)2ε0DNone of these
A∮s(→E1+→E2+→E3).d→A=q1+q2+q32ε0B∮s(→E1+→E2+→E3).d→A=(q1+q2+q3)ε0C∮s(→E1+→E2+→E3).d→A=(q1+q2+q3+q4)2ε0DNone of theseA charge +Q is uniformly distributed along the circular arc of radius R as shown in the figure.The magnitude of the force experienced by the point charge +q place at the centre of curvature is (k=14πε0)
 AkQqsinθ2R2θB2kQqsinθ2R2θC2kQqcosθ2R2θD2kQqtanθ2R2θ
AkQqsinθ2R2θB2kQqsinθ2R2θC2kQqcosθ2R2θD2kQqtanθ2R2θ
A point charge +Q is placed at a distance r from a short dipole of dipole moment →p as shown in figure. The line joining the point charge Q to the centre dipole is perpendicular to dipole moment →p, which of the following statement are true?AThe net electrostatics force on the dipole is zeroBThe electrostatics force on the dipole in Qp4πε0r3 and is acting along the dipole moment →p.CTorque acting on dipole is Qp4πε0r2 in inward direction.Dtorque acting on the dipole is Qp2πε0r2 in inward direction.
A charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).

View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
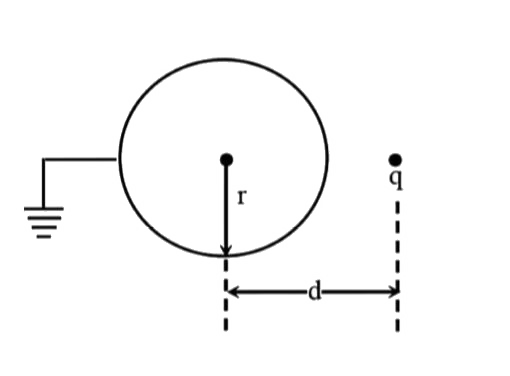
View SolutionThe point charge is placed outside a spherical shell as shown i the figure. Find the electric potential (in kilo volt) on the surface of shell (Take: q=1μc and R=50cm)

View SolutionIf a charge q is placed at the centre of imaginary sphere of radius r then the N.E.I. at a point on such a sphere is
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View Solution

