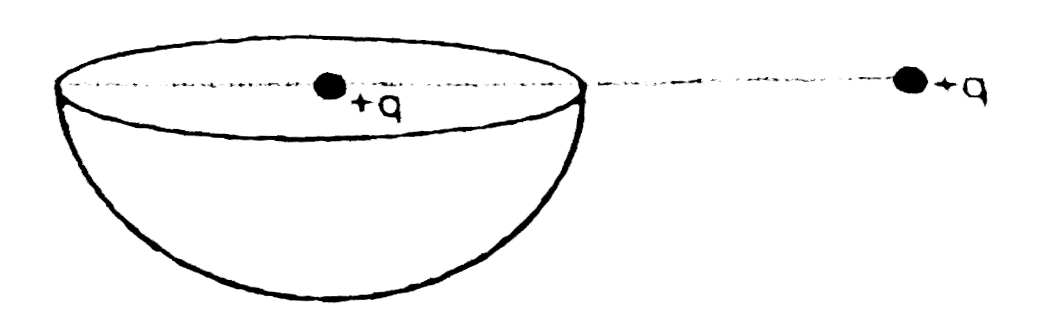
A charge q is situated at the centre of an imaginary hemispherical surface, as shown in figure. Using gauss's theorem and symmetry considerations, determine the electric flux due to this charge through the hemisphere surface.
The correct Answer is:q2ε0
Step by step video, text & image solution for A charge q is situated at the centre of an imaginary hemispherical surface, as shown in figure. Using gauss's theorem and symmetry considerations, determine the electric flux due to this charge through the hemisphere surface. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBook:SL ARORAChapter:ELECTRIC POTENTIAL AND ELECTRIC FLUXExercise:Problem
Explore 15 Videos
- CURRENT ELECTRICITYBook:SL ARORAChapter:CURRENT ELECTRICITYExercise:Problems For Self
Explore 101 Videos
- ELECTRICAL INSTRUMENTSBook:SL ARORAChapter:ELECTRICAL INSTRUMENTSExercise:Problem for self practice
Explore 81 Videos
Similar Questions
Knowledge Check
The flux of electric field due to these charges through the surface S is
 A2qε0B3qε0C−5qε0Dqε0
A2qε0B3qε0C−5qε0Dqε0Find the total flux due to charge q associated with the given hemispherical surface
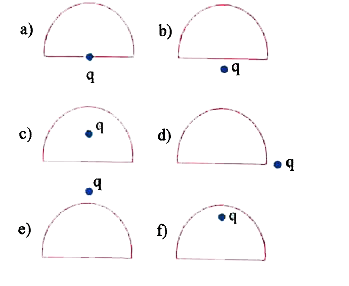 A(a)q2ε0,(b)0,(c)qε0,(d)0,(e)0(f)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0(f)qε0C(a)q2ε0,(b)qε0,(c)0,(d)qε0,(e)0(f)qε0D(a)0,(b)q2ε0,(c)0(d)qε0,(e)qε0(f)qε0
A(a)q2ε0,(b)0,(c)qε0,(d)0,(e)0(f)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0(f)qε0C(a)q2ε0,(b)qε0,(c)0,(d)qε0,(e)0(f)qε0D(a)0,(b)q2ε0,(c)0(d)qε0,(e)qε0(f)qε0A charge q is located at the centre of a cube. The electric flux through any face is
Aπq6(4π∈0)Bq6(4π∈0)C2πq6(4π∈0)D4πq6(4π∈0)
A charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).

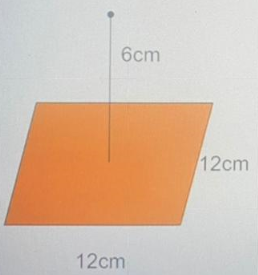
View SolutionFind the flux of point charge q through the square surface ABCD as shown
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionFind the total flux due to charge qassociated with the given hemisphercal surface
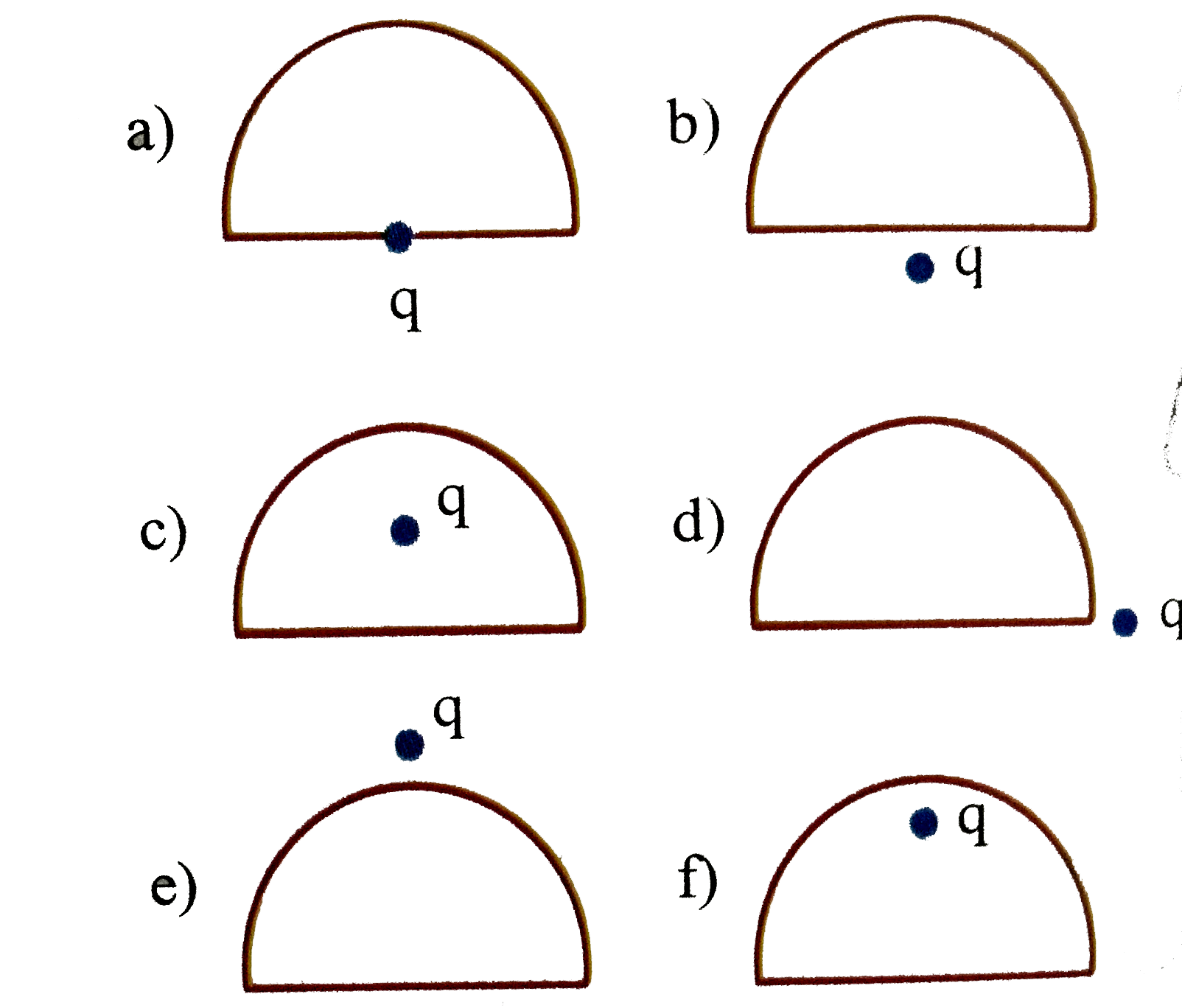
View Solution