Two bodies of masses M and 27 M are allowed to fall on a viscous liquid simultaneously. The respective terminal velocities of bodies are V and kV. The value of k is
5
7
8
9
The correct Answer is:D
To solve the problem, we need to find the value of k in the context of two bodies falling through a viscous liquid, where one body has a mass M and the other has a mass 27M. The terminal velocities of these bodies are V and kV respectively.
1. Understand the Terminal Velocity Formula:
The terminal velocity Vt of an object falling through a viscous fluid is given by the formula:
Vt=29r2(ρ−σ)gη
where:
- r = radius of the object,
- ρ = density of the object,
- σ = density of the fluid,
- g = acceleration due to gravity,
- η = viscosity of the fluid.
2. Relate Mass and Volume:
The density ρ of the bodies can be expressed as:
ρ=MV
where V is the volume of the body. The volume of a sphere is given by V=43πr3. Thus, we can express the density in terms of radius:
ρ=M43πr3⟹ρ∝Mr3
3. Set Up the Ratios:
For the two bodies, let:
- Body 1 (mass M): terminal velocity V
- Body 2 (mass 27M): terminal velocity kV
Using the terminal velocity formula, we can write:
V∝r21(ρ1−σ)gη
kV∝r22(ρ2−σ)gη
4. Density Relation:
Since the density of the fluid σ is constant, we can relate the densities of the two bodies:
ρ1=M43πr31,ρ2=27M43πr32
Thus,
ρ1ρ2=M/43πr3127M/43πr32=r3227r31
5. Volume Ratio:
Since the densities are equal at terminal velocity, we can set up the ratio:
r31r32=127⟹r1r2=13
6. Terminal Velocity Ratio:
Now, substituting this ratio into the terminal velocity equations:
VkV=r21r22=(13)2=19
Thus, we have:
1k=19⟹k=9
Conclusion:
The value of k is 9.
The terminal velocity Vt of an object falling through a viscous fluid is given by the formula:
Vt=29r2(ρ−σ)gη
where:
- r = radius of the object,
- ρ = density of the object,
- σ = density of the fluid,
- g = acceleration due to gravity,
- η = viscosity of the fluid.
The density ρ of the bodies can be expressed as:
ρ=MV
where V is the volume of the body. The volume of a sphere is given by V=43πr3. Thus, we can express the density in terms of radius:
ρ=M43πr3⟹ρ∝Mr3
For the two bodies, let:
- Body 1 (mass M): terminal velocity V
- Body 2 (mass 27M): terminal velocity kV
V∝r21(ρ1−σ)gη
kV∝r22(ρ2−σ)gη
Since the density of the fluid σ is constant, we can relate the densities of the two bodies:
ρ1=M43πr31,ρ2=27M43πr32
Thus,
ρ1ρ2=M/43πr3127M/43πr32=r3227r31
Since the densities are equal at terminal velocity, we can set up the ratio:
r31r32=127⟹r1r2=13
Now, substituting this ratio into the terminal velocity equations:
VkV=r21r22=(13)2=19
Thus, we have:
1k=19⟹k=9
The value of k is 9.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
Explore 6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (JEE (Main) & Other State Boards For Engineering Entrance)
Explore 23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Revision Exercise (Numerical Problems)
Explore 28 Videos
- MATHEMATICAL TOOLSBook:MODERN PUBLICATIONChapter:MATHEMATICAL TOOLSExercise:PRACTICE PROBLEMS (10)
Explore 12 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
Similar Questions
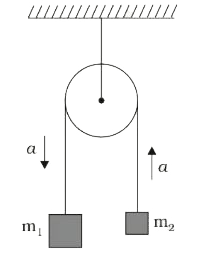
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
View SolutionTwo bodies of masses M and m are allowed to fall from the same height . If air resistance for each body be same , will the two bodies reach the ground simultaneously ?
View Solution
Knowledge Check
Two solid spheres of same metal but of mass M and 8M fall simultaneously on a viscous liquid and their terminal velocitied are v and n v, then value of n is
A16B8C4D2Two solid spheres of same metal but of mass M and 8M fall simultaneously on a viscous liquid and their terminal velocities are v and nv, then value of n is
A16B8C4D2Two solid spheres of came metal bar of mass 8M and 27M fall simultaneouslyon a viscous liquid and their terminal velocities are v and nv, then values n is
A16B8.5C4D2.25
Two bodies of masses M and m are allowed to fall from the same height. If air resistance for each body be same, will the two bodies reach the ground simultaneously ?
View Solutioni) If the net force acting on a body is zero, will it remain necessarily at rest?
(ii) Two bodies of mass M and m are allowed to fall from the same height. If air resistance for each body be same, will the two bodies reach the ground simultaneously?
View SolutionAssertion: Two bodies of masses M and m(M>m) are allowed to fall from the same height if the air resistance for each be the same then both the bodies will reach the earth simultaneously.
Reason: For same air resistance, acceleration of both the bodies will be same.
View SolutionAssertion: Two bodies of masses M and m(M>m) are allowed to fall from the same height if the air resistance for each be the same then both the bodies will reach the earth simultaneously.
Reason: For same air resistance, acceleration of both the bodies will be same.
View SolutionA sperical body of mass m and radius r is allowed to fall in a medium of viscosity η. The time in which the velocity of the body increases from zero to 0.63 times the terminal velocity (v) is called constant (τ). Dimensionally , τ can be represented by
View Solution

