One third of a cylinder of 3 m height is filled with oil of density 0.62 g cm−3. and the rest of it is filled with mercury of density 13.6 g cm−3. Calculate the total pressure at the bottom of cylinder due to both oil and mercury.
To solve the problem, we need to calculate the total pressure at the bottom of the cylinder due to both the oil and mercury. We will follow these steps:
Step 1: Understand the Heights of the Fluids
The total height of the cylinder is 3 m. Since one third of the cylinder is filled with oil, the height of the oil column is:
hoil=13×3m=1m
The remaining height, which is filled with mercury, is:
hmercury=3m−1m=2m
Step 2: Convert Densities to SI Units
The densities of the fluids are given in g/cm³, and we need to convert them to kg/m³ for SI units:
- Density of oil:
ρoil=0.62g/cm3=0.62×103kg/m3=620kg/m3
- Density of mercury:
ρmercury=13.6g/cm3=13.6×103kg/m3=13600kg/m3
Step 3: Calculate the Pressure Due to Mercury
The pressure at the bottom of the cylinder due to the mercury can be calculated using the formula:
Pmercury=ρmercury⋅g⋅hmercury
Assuming g=10m/s2:
Pmercury=13600kg/m3⋅10m/s2⋅2m=272000Pa
Step 4: Calculate the Pressure Due to Oil
The pressure at the bottom of the cylinder due to the oil is:
Poil=ρoil⋅g⋅hoil
Poil=620kg/m3⋅10m/s2⋅1m=6200Pa
Step 5: Calculate the Total Pressure at the Bottom
The total pressure at the bottom of the cylinder is the sum of the pressures due to both the oil and mercury:
Ptotal=Pmercury+Poil=272000Pa+6200Pa=278200Pa
Final Answer
The total pressure at the bottom of the cylinder due to both oil and mercury is:
278200Pa
The total height of the cylinder is 3 m. Since one third of the cylinder is filled with oil, the height of the oil column is:
hoil=13×3m=1m
The remaining height, which is filled with mercury, is:
hmercury=3m−1m=2m
The densities of the fluids are given in g/cm³, and we need to convert them to kg/m³ for SI units:
- Density of oil:
ρoil=0.62g/cm3=0.62×103kg/m3=620kg/m3
- Density of mercury:
ρmercury=13.6g/cm3=13.6×103kg/m3=13600kg/m3
The pressure at the bottom of the cylinder due to the mercury can be calculated using the formula:
Pmercury=ρmercury⋅g⋅hmercury
Assuming g=10m/s2:
Pmercury=13600kg/m3⋅10m/s2⋅2m=272000Pa
The pressure at the bottom of the cylinder due to the oil is:
Poil=ρoil⋅g⋅hoil
Poil=620kg/m3⋅10m/s2⋅1m=6200Pa
The total pressure at the bottom of the cylinder is the sum of the pressures due to both the oil and mercury:
Ptotal=Pmercury+Poil=272000Pa+6200Pa=278200Pa
The total pressure at the bottom of the cylinder due to both oil and mercury is:
278200Pa
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (A. MCQ (Objectie Type Questions))
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Long Answer Questions)
7 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Knowledge Check
A tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2A tank 5 m high is half filled with water and then is filled to the top with oil of density 0.85 g The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2What is the barometric height of a liquid of density 3.4 g cm−3 at a place, where that for mercury barometer is 70 cm?
A70 cmB140 cmC280 cmD340 cm
What volume will 250 g of mercury occupy ? (Density of mercury =13.6 g cm−3)
View SolutionThe density of mercury is 13.6 g cm−3 in CGS system. Find its value in SI units.
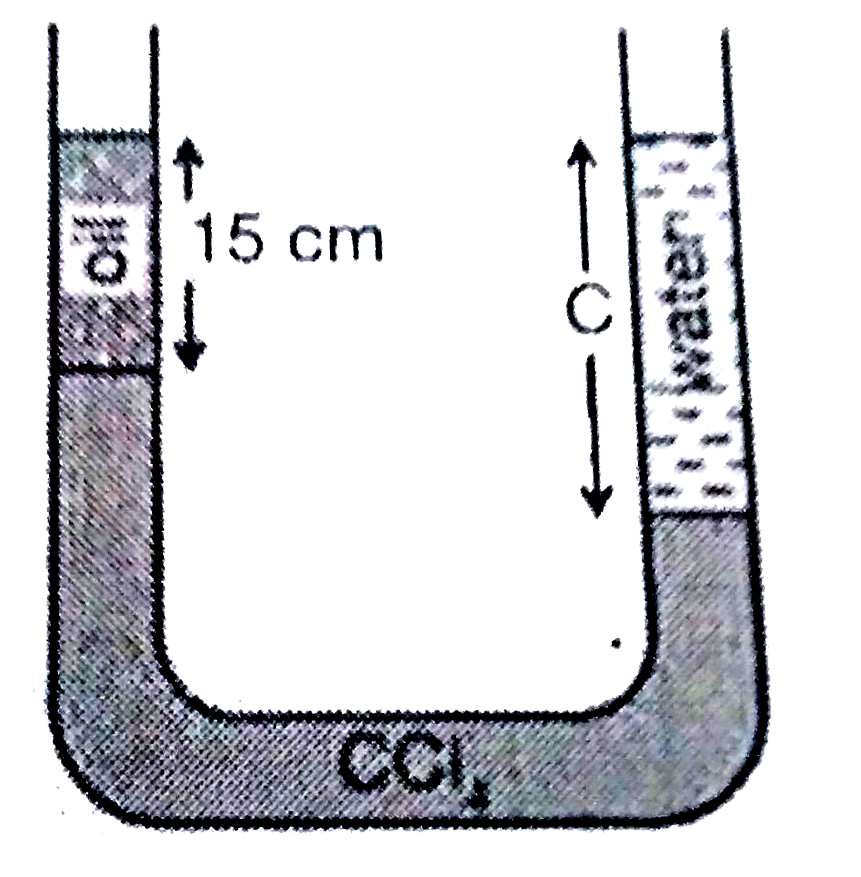
View SolutionA 'U' tube contains oil, carbon tetrachloride and water as shown in the figure. The density of oil is 0.8 g cm−3 and that of carbon tetrachloride is 1.6g cm−3. If oil and water surfaces are at the same level, find the height of the water column.
View SolutionA vertical U tube has two limbs of unequal radii are 5 cm and 0.1 respectively . The tube is partly filled with mercury of density 13.6 g/cm3 and surface tension is 550 dyne /cm . Assume the two levels of the limbs is
View SolutionDensity of mercury is 13.6gcm−3. Its density in kg m−3 is
View Solution
