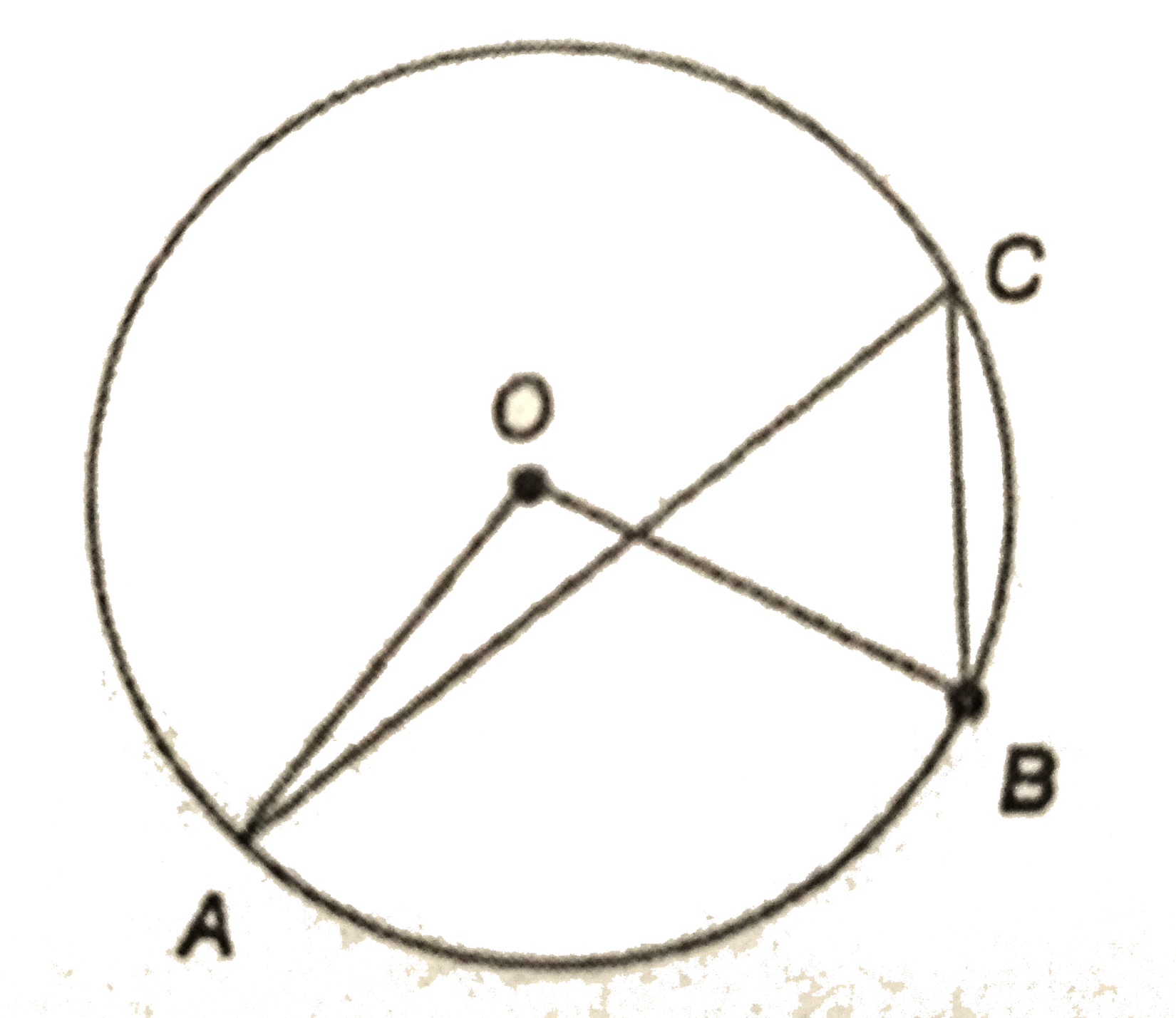
In the figure, A,B,E,C and D are the points on the circle. If AB=BE and ∠ACB=30∘ , then find ∠ADE.
A
50∘
B
45∘
C
60∘
D
80∘
Video Solution
Text Solution
The correct Answer is:c
∠ACB=30∘ (given )
Let 'O' be the centre of the circle.
⇒∠AOB=60∘,∠BOE=∠AOB (∵AB=BE)
∴∠AOE=60∘+60∘=120∘
∴∠ADE=120∘2=60∘
|
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 3
Explore 7 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
Explore 28 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 1
Explore 32 Videos
- FormulaeBook:PEARSON IIT JEE FOUNDATIONChapter:FormulaeExercise:Level 3
Explore 7 Videos
- INDICESBook:PEARSON IIT JEE FOUNDATIONChapter:INDICESExercise:CONCEPT APPLICATION (Level 3)
Explore 7 Videos
Similar Questions
Knowledge Check
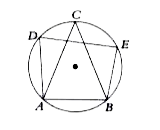
In the figure , A,B,C,andD are the points on the circle .If AB =BE and ∠ACB=30∘ , then find ∠ADE .A30∘B45∘C60∘D80∘In the figure, CDE is a straight line and A, B, C and D are points on the circle. ∠BCD=44∘, find the value of x.
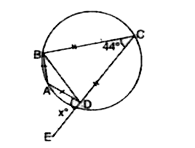 A44∘B68∘C90∘D56∘
A44∘B68∘C90∘D56∘In the figure , if AD, AE and BC are tangent to the circle at D,E and F , respectively , then
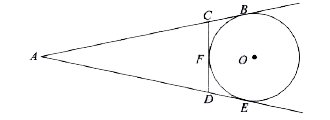 AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CA
AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CA
In the adjoining figure 'O' is the center of the circle AB=BCm∠AOD=xandm∠ACB=y then find xy.
View Solution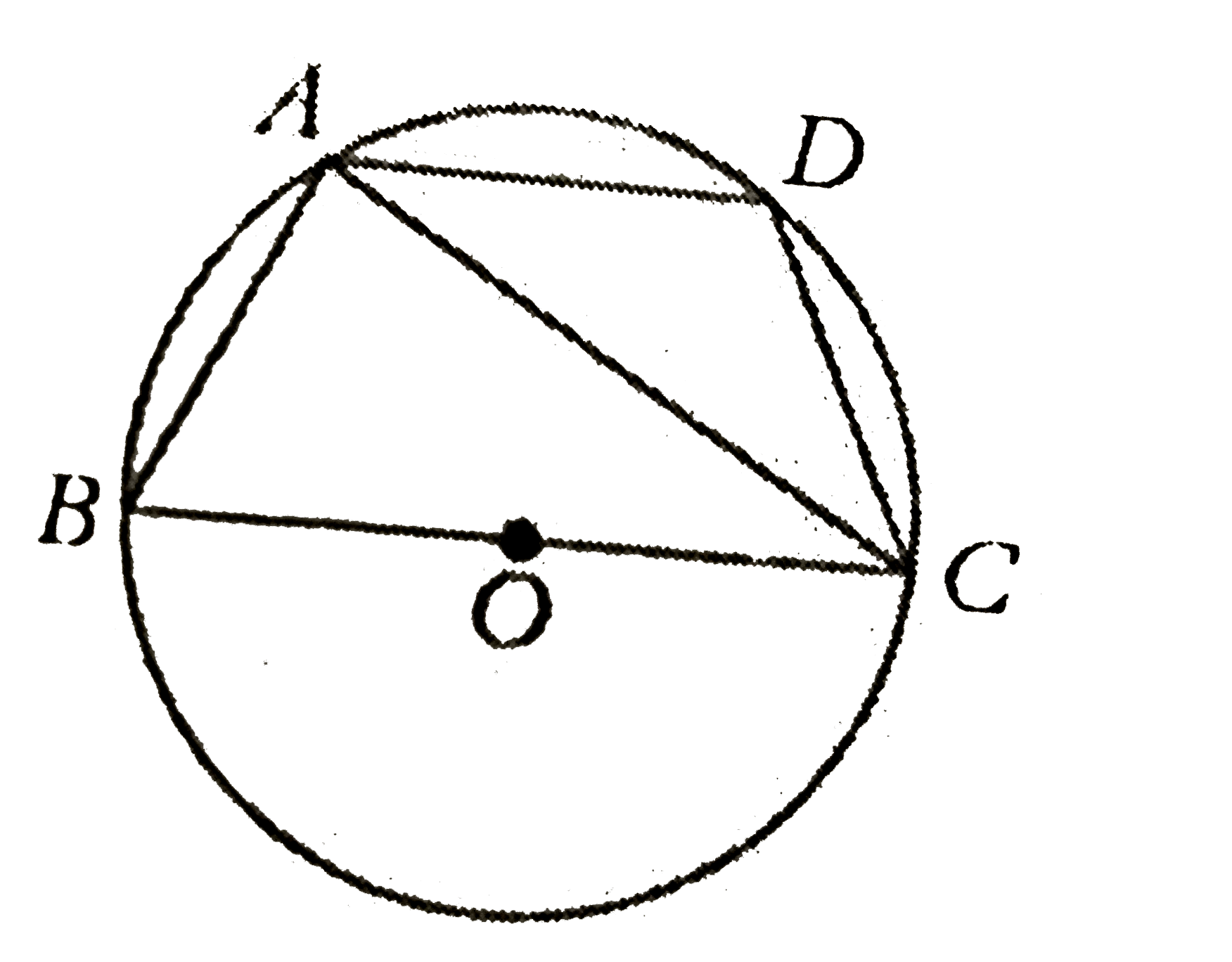
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View Solution
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACB
View Solution
In the figure above ,AD=AC=BD. The point B, D and C are collinear. If ∠CAD=80∘, then find ∠DAB.
View SolutionIn the diagram, A, B, C, D, E are points on the circle. AB||DC, ∠ADE=39∘and∠ABC=62∘. Then the values of x and y respectively are :
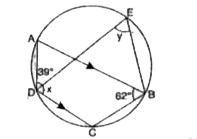
View Solution