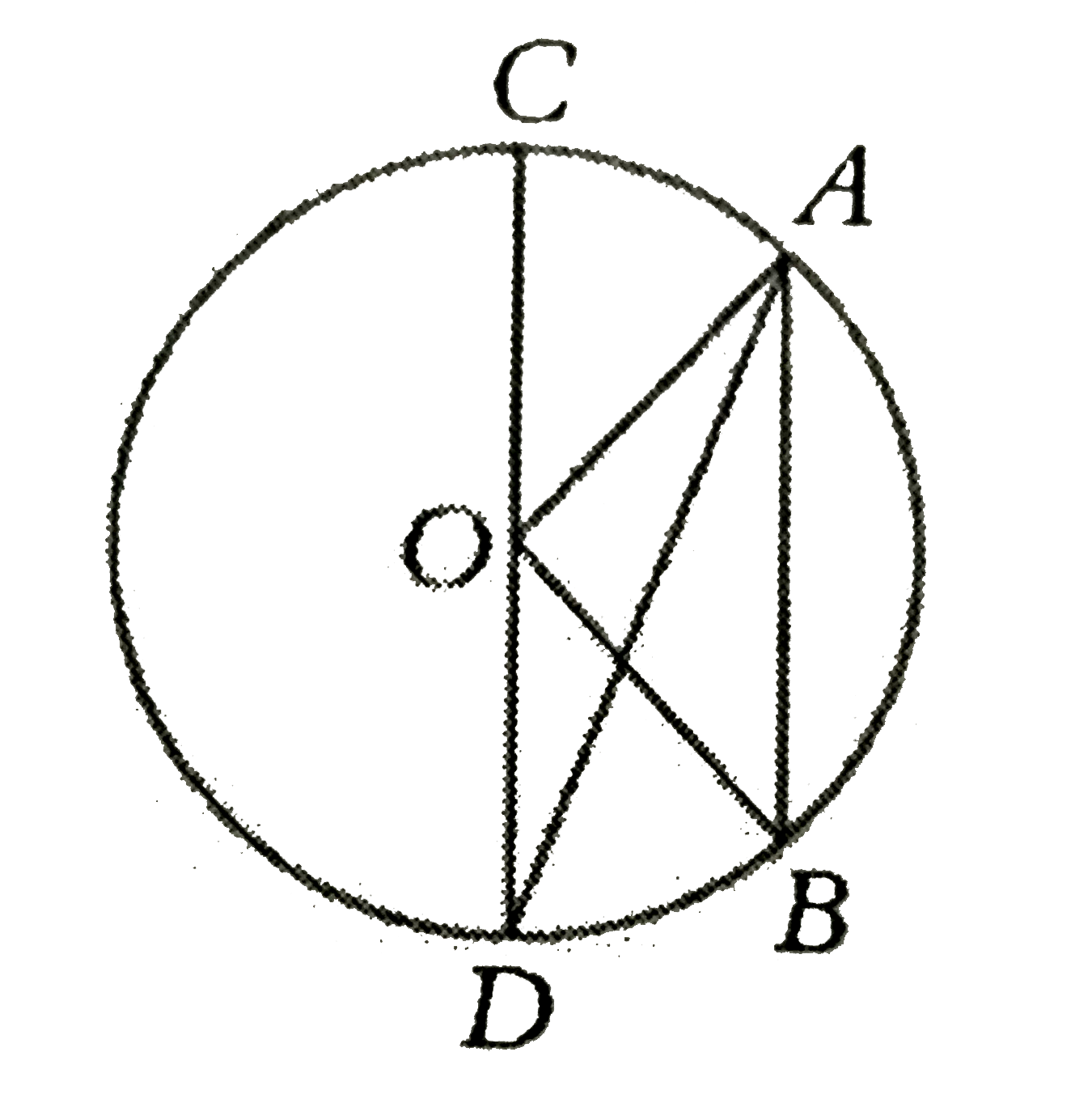
In the above figure (not to scale) , O is the centre of the circle and ¯¯¯¯¯¯CD∣∣¯¯¯¯¯¯AB. If ∠DAO=20∘, then ∠AOB=
110∘
130∘
100∘
120∘
The correct Answer is:c
(i) Join AC and BD to form a cyclic quadrilateral.
(ii) ΔACD is a right triangle as ¯¯¯¯¯¯CD is diameter.
(iii) ∠DAB=40∘ and ΔAOB is isosceles.
Using these, find the required angle.
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 3
Explore 7 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
Explore 28 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 1
Explore 32 Videos
- FormulaeBook:PEARSON IIT JEE FOUNDATIONChapter:FormulaeExercise:Level 3
Explore 7 Videos
- INDICESBook:PEARSON IIT JEE FOUNDATIONChapter:INDICESExercise:CONCEPT APPLICATION (Level 3)
Explore 7 Videos
Similar Questions
Knowledge Check
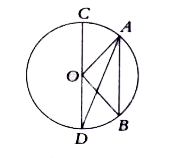
In the above figure (not to scale) , O is the centre of the circle and ¯¯¯¯¯¯CD∣∣¯¯¯¯¯¯AB.If ∠DAO=20∘ , then ∠AOB= _______.A110∘B130∘C100∘D120∘In the given figure (not to scale ) , O is the centre of the circle . A ,B,C and D are conyclic and AB =CD . If ∠MON=120∘ , then find ∠OPN .
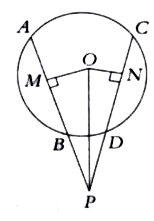 A20∘B30∘C40∘D60∘
A20∘B30∘C40∘D60∘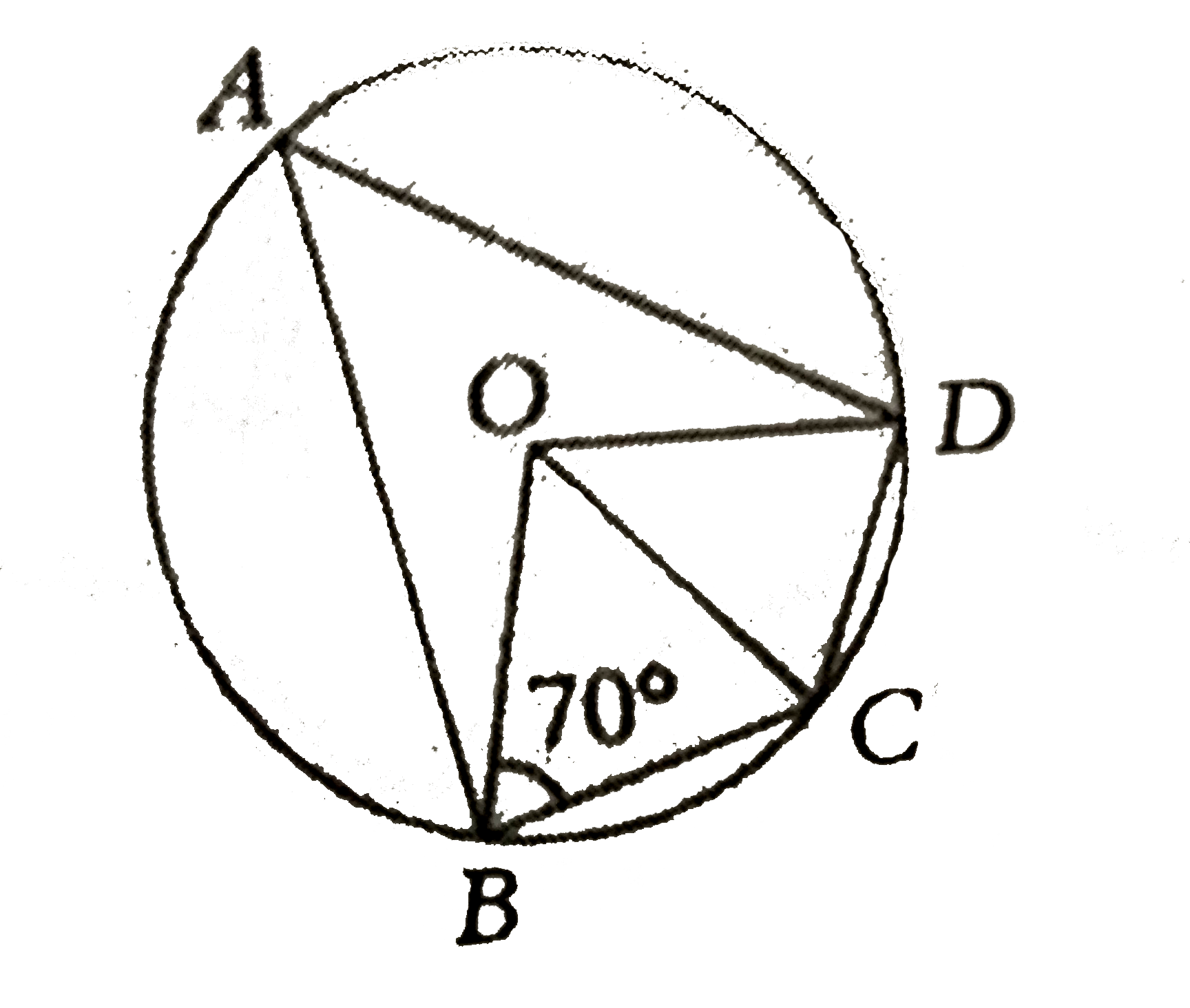
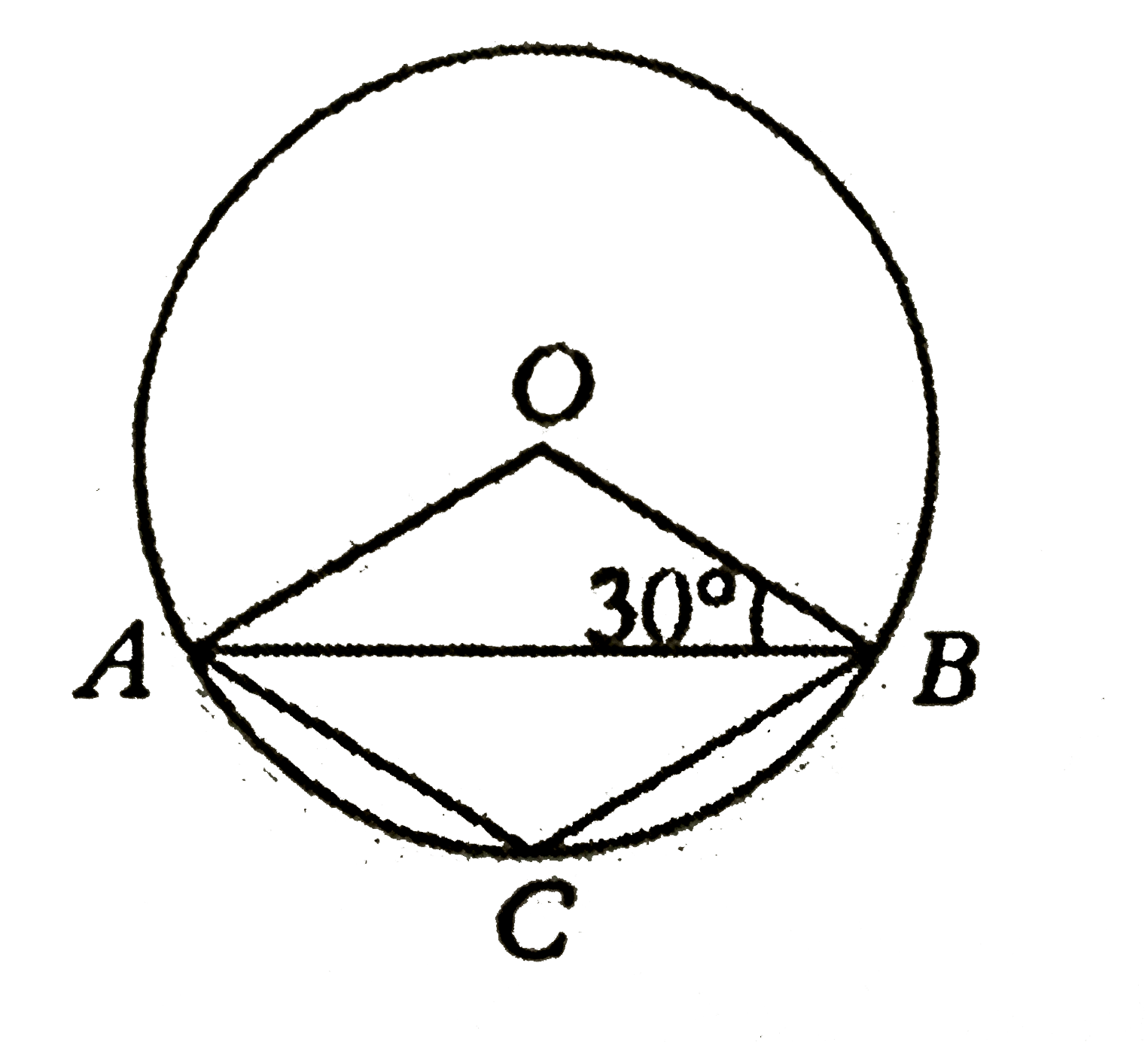
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯BC and ¯¯¯¯¯¯CD are equal chords. If ∠OBC=70∘ , then find ∠BAD.A40∘B60∘C55∘D45∘
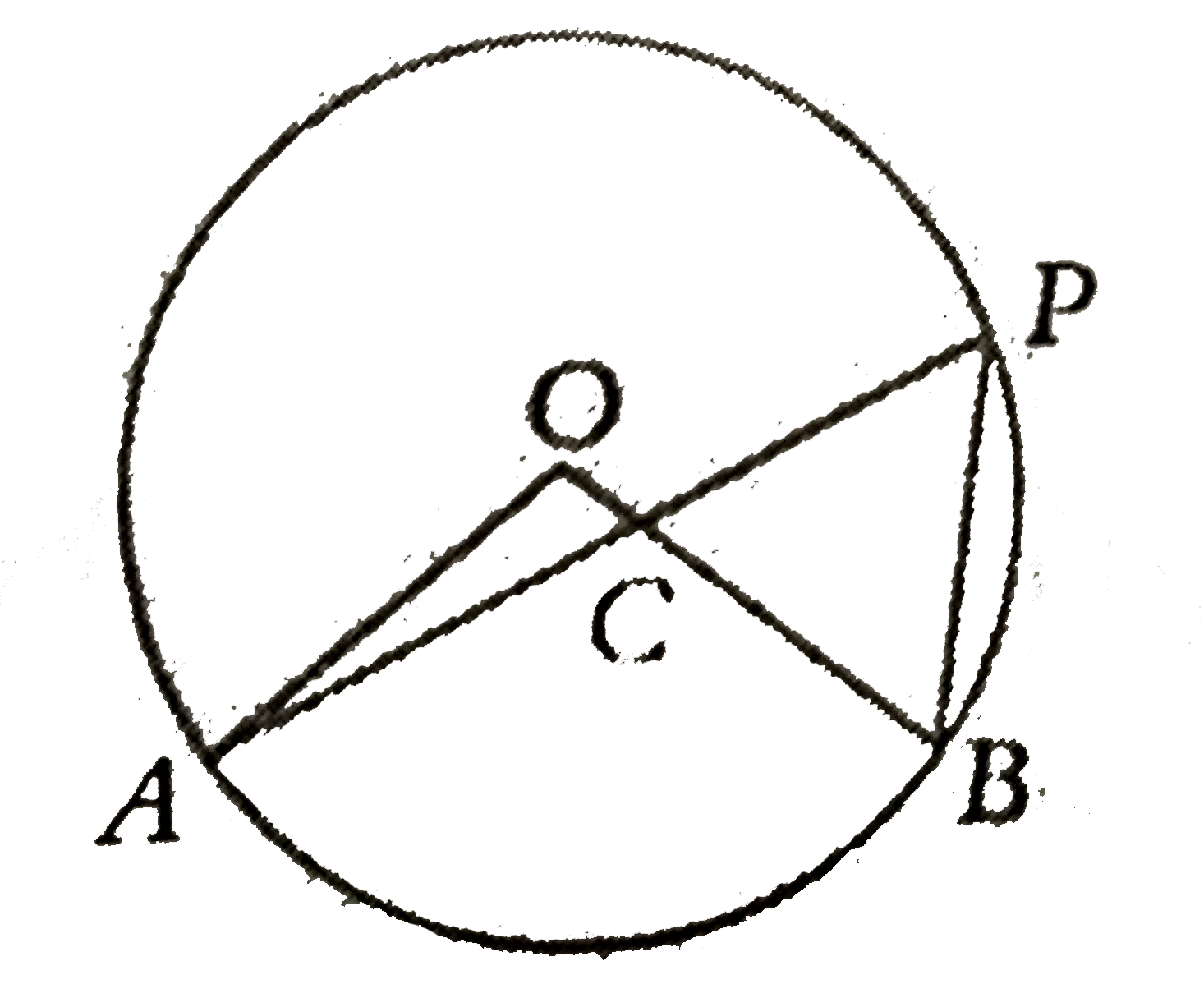
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯AP and ¯¯¯¯¯¯BP are two chords. C is the point of intersection of ¯¯¯¯¯¯AP and ¯¯¯¯¯¯OB. If ∠OAC=30∘ and ∠PBC=80∘, then ∠AOB=
View Solution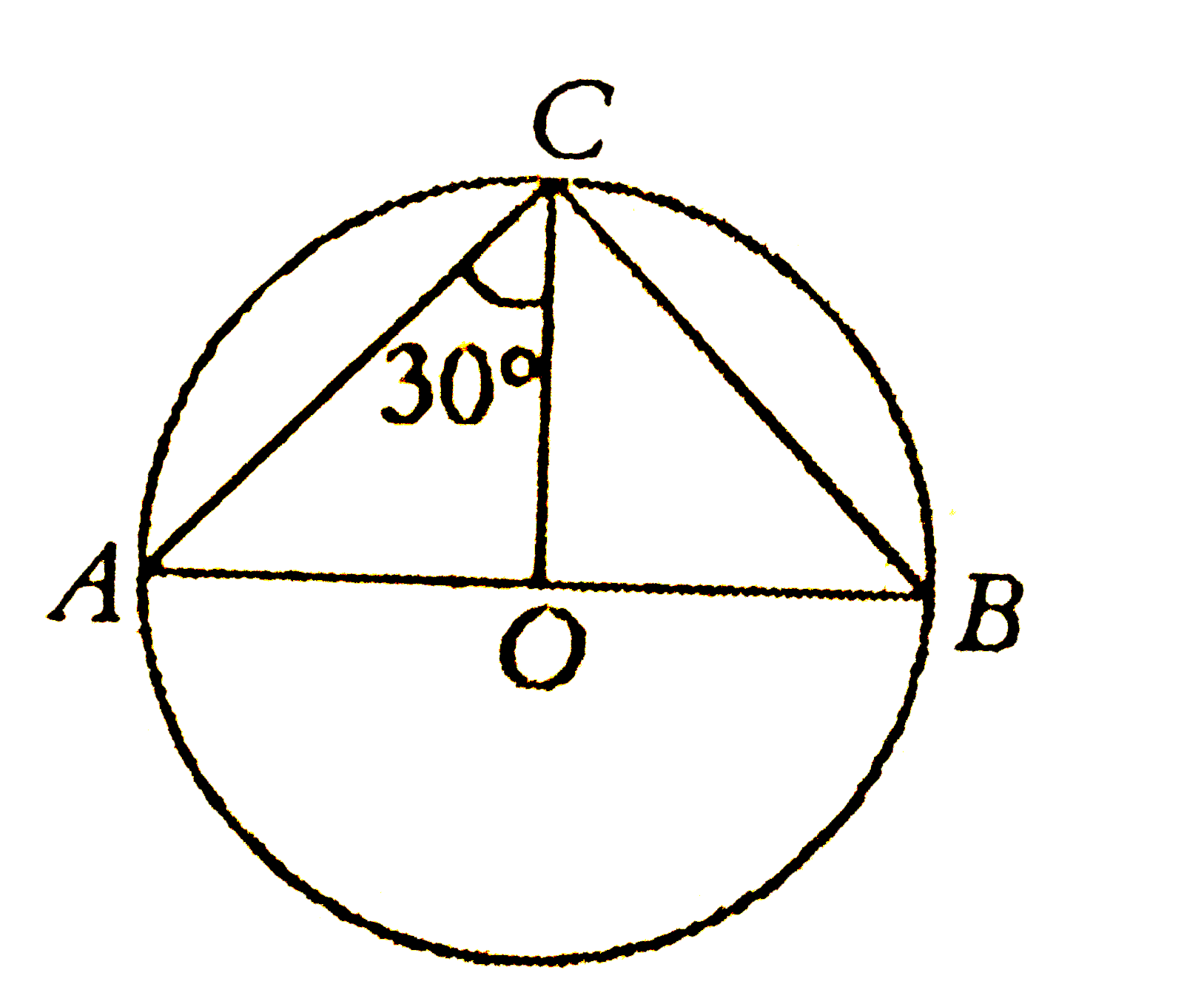
In the figure above (not to scale), AB is the diameter of the circle with centre O. If ∠ACO=30∘, then find ∠BOC.
View Solution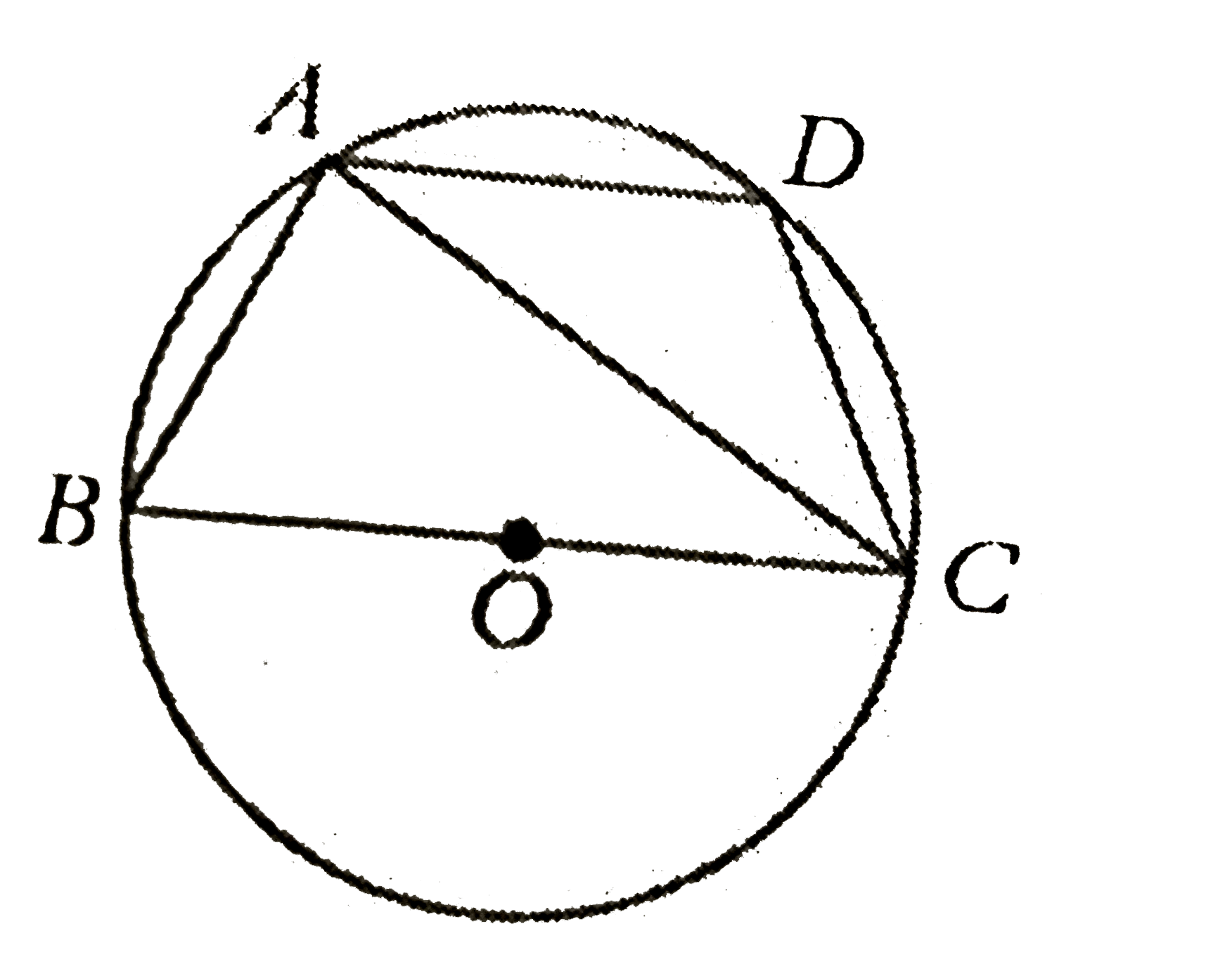
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View SolutionIn the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
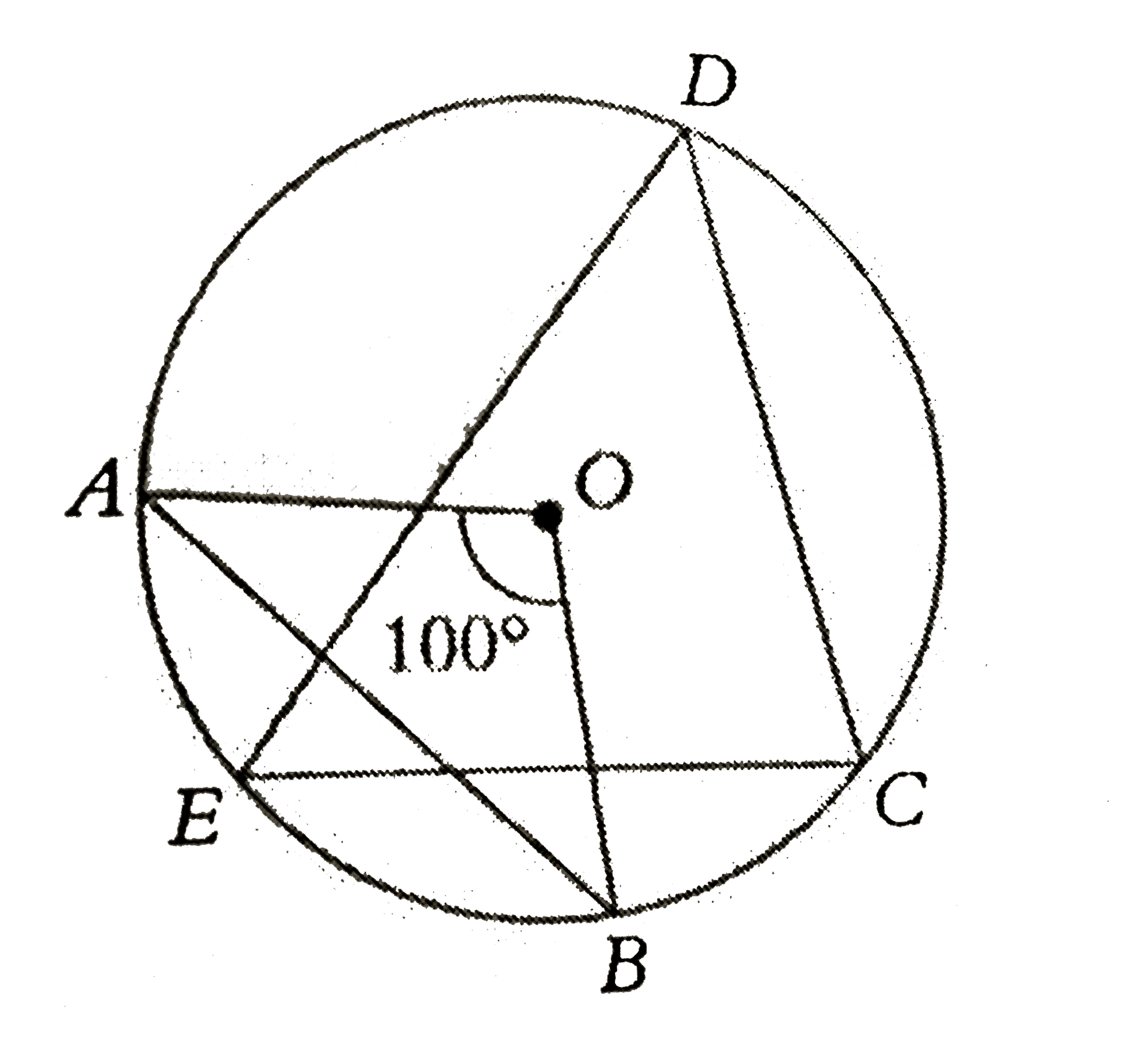
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.
View Solution