The perpenidicular drawn from the centre of a circle bisects any chord of the circle. The following are the steps involved in proving the above result. Arrange them in sequential order.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VIII_C16_E05_015_Q01.png" width="80%"gt
(A) Let .
(B) Let AB be the chord of the circle with centre O.
(C ) ( By RHS congruence property).
(D ) (radii), ( common side) and
(E ) ( corresponding parts in congurents triangles ).
A
BADCE
B
BCDAE
C
DBACDE
D
BDEAC
Video Solution
Text Solution
The correct Answer is:a
and is the required sequential order.
|
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 3
Explore 7 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
Explore 28 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level 1
Explore 32 Videos
- FormulaeBook:PEARSON IIT JEE FOUNDATIONChapter:FormulaeExercise:Level 3
Explore 7 Videos
- INDICESBook:PEARSON IIT JEE FOUNDATIONChapter:INDICESExercise:CONCEPT APPLICATION (Level 3)
Explore 7 Videos
Similar Questions
Match the following Column A to Column B

View SolutionMatch the following Column A to Column B

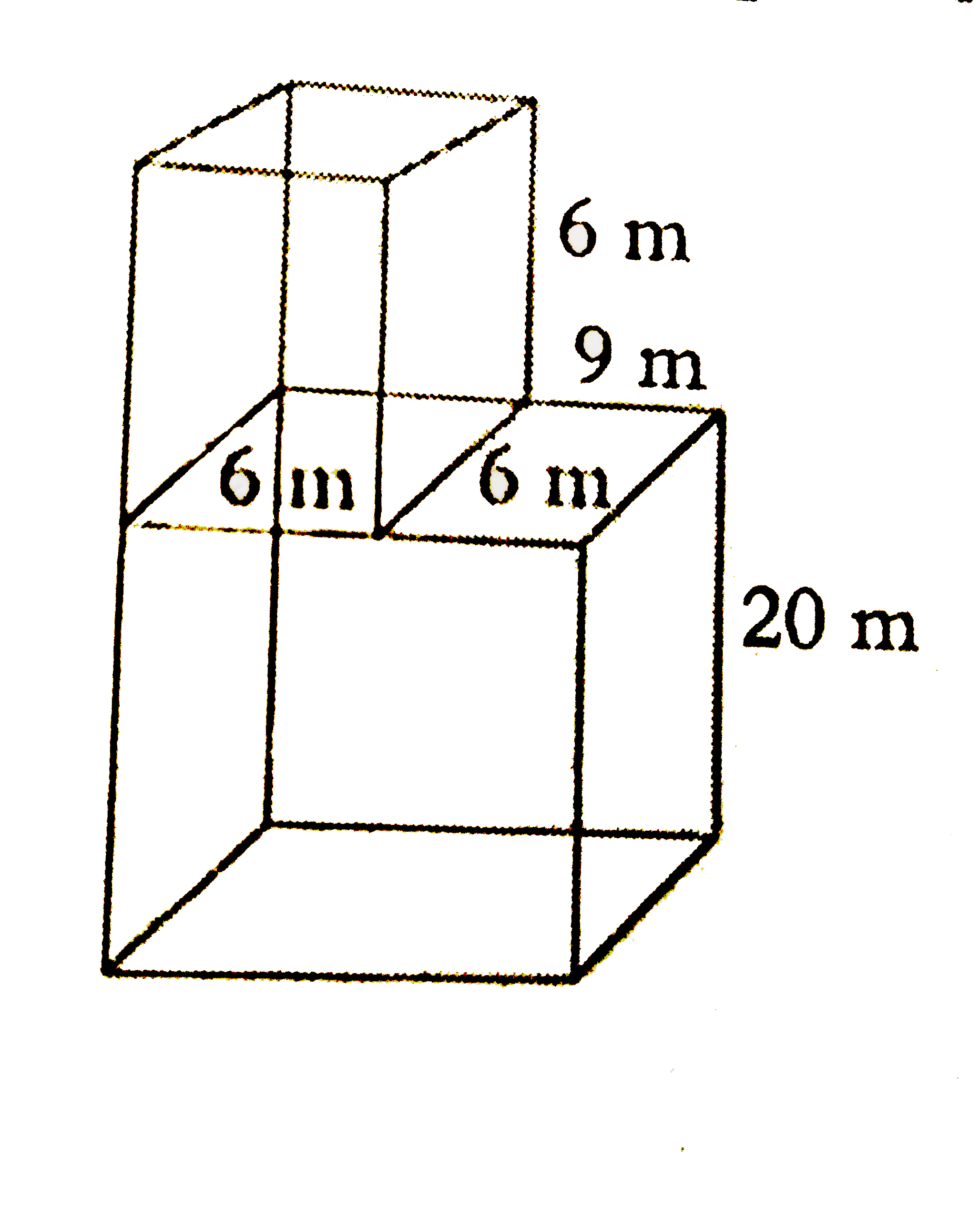
View SolutionCalculate the volume of the given solid.
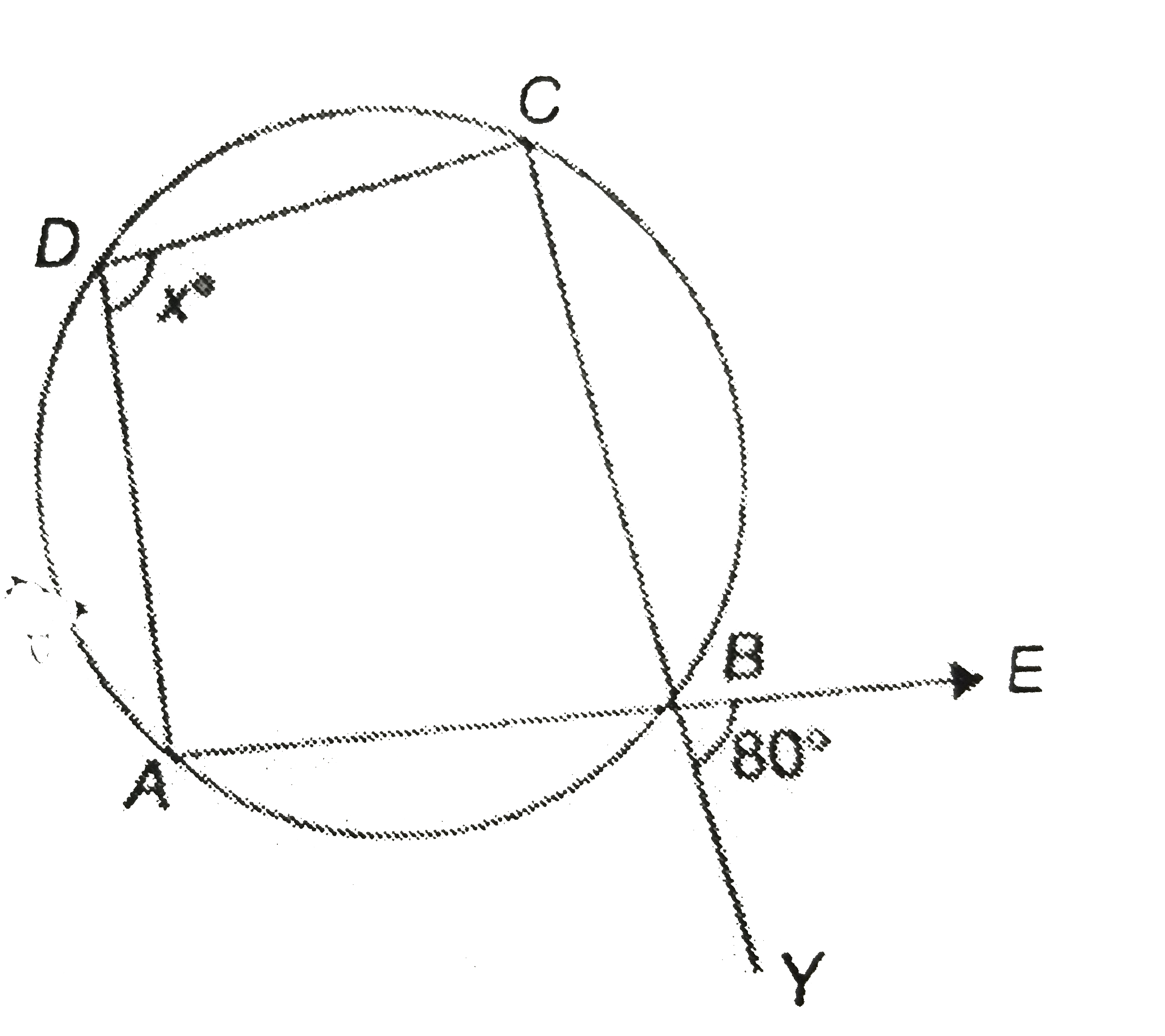
View SolutionIn Fig, find the value of x.
View SolutionDraw the bisector of ∠AOB=58∘

View SolutionFind the area of the figure given below.

View SolutionFind the area of figure given below.
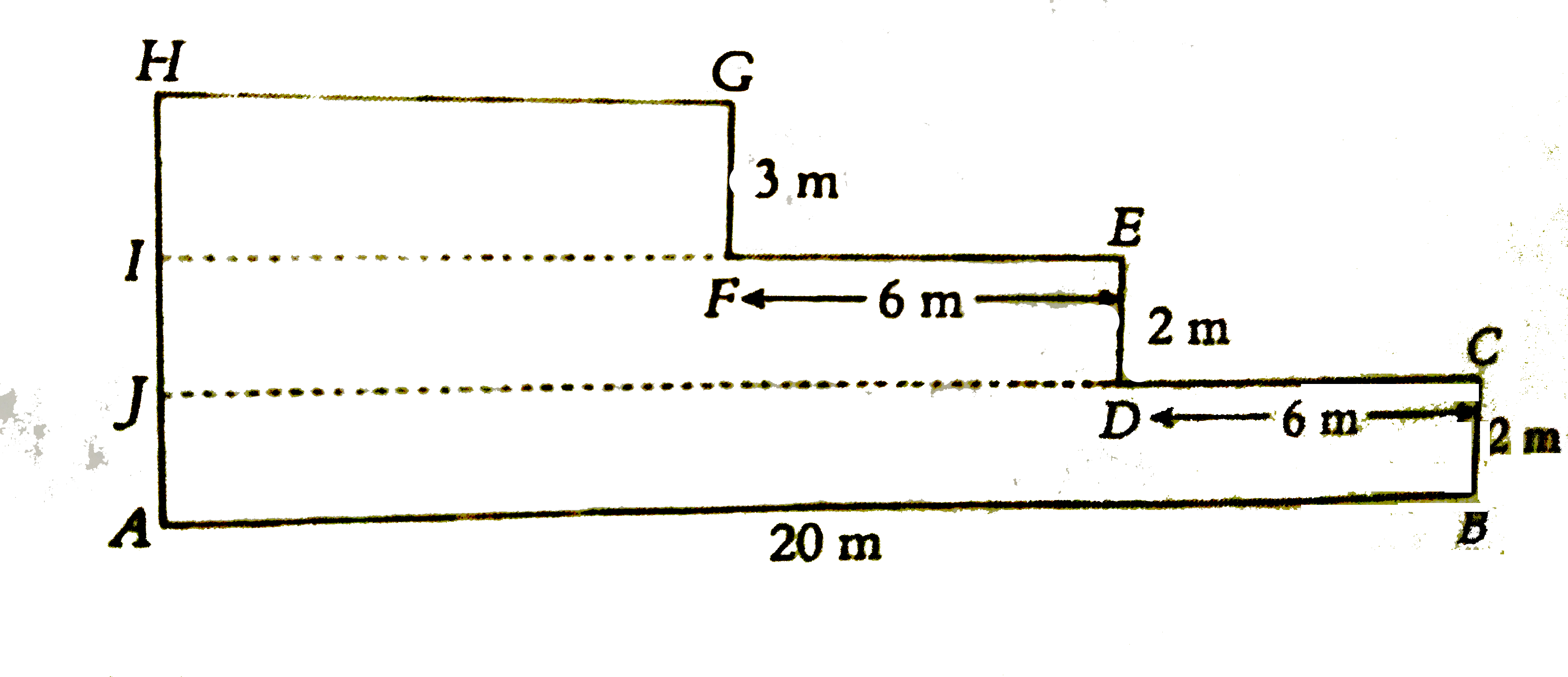
View SolutionFind the perimeter of the figure given below.
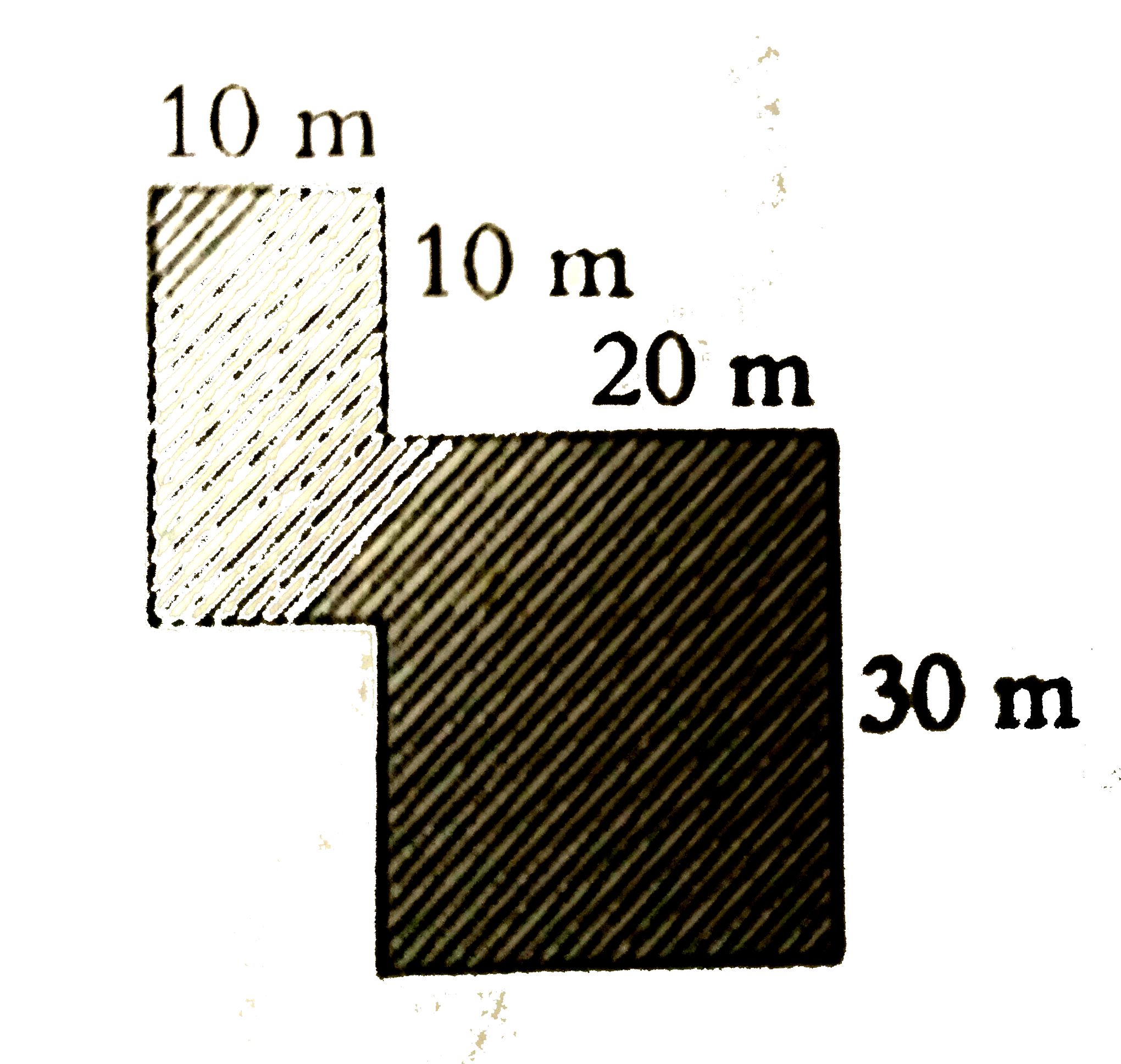
View SolutionIdentify the cell organelle 'A' :-

View SolutionThe area of the shaded part in the figure given below is ______.

View Solution
