Light of two different frequencies whose photons have energies 1 eV and 2.5 eV respectively, successively illuminate a metallic surface whose work function is 0.5 eV. Ratio of maximum speeds of emitted electrons will beSolution in Kannada
1:4
1:1
1:5
1:2
The correct Answer is:D
According to Einstein's photogenic equation , the maximum kinetic energy of emitted photoelectrons is
Kmax=hv−ϕ0
where hv is the energy of incident and ϕ0 is the work function .
But Kmax=12mv2max
∴12mv2max=h∨−ϕ0
As per equation
12mvmax=1eV−0.5eV=0.5eV....(i)
and and12mv2max2=2.5eV−0.5eV=2eV ...(ii)
Dividing eqn . (i) by eqn . (ii) , we get
v2max1v2max2=0.5eV2eV=14
vmax1vmax2=√14=12
Topper's Solved these Questions
Similar Questions
A solenoid length 0.4cm, radius 1 cm and 400 turns of wire. If a current of 5 A is passed through this solenoid, what is the magnetic field inside the solenoid ?
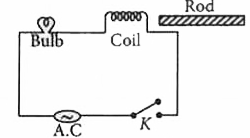
View SolutionIn the A. C. circuit shown, keeping 'K' pressed, if an iron rod is inserted into the coil, the bulb in the circuit
View SolutionLights of two different frequencies whose photons have energies 1 and 2.5 eV, respectively, successively illuminate a metal whose work function is 0.5 eV. The ratio of the maximum speeds of the emitted electrons
View SolutionLight of two different frequencies whose photons have energies 1eV and 2.5 eV respectively illuminate a metallic surface whose work function is 0.5 eV successively. Ratio of maximum kinetic energy of emitted electrons will be:
View SolutionLights of two different frequencies whose photons have energies 1 eV and 2.5 eV respectively illuminate successively a metal surface whose work function is 0.6 eV. The ratio of the maximum speeds of the emitted electrons will have
View SolutionLights of two different frequencies, whose photons have energies 1 eV and 2.5 eV respectively, successively illuminate a metal whose work function is 0.5 eV. The ratio of the maximum speeds of the emitted electrons will be
View SolutionLight of two different frequencies whose photons have energies 1 eV and 2.5 eV respectively, successively illuminate a metallic surface whose work function is 0.5 eV. Ratio of maximum speeds of emitted electrons will be
View SolutionLight of two different frequencies whose photons have energies 1 eV and 2.5 eV respectively illuminate a metallic surface whose work function is 0.5 eV successively. Find the ratio of maximum speeds of emitted electrons.
View SolutionLights of two different frequencies whose photons have energies 1 and 2.5 eV, respectively, successively illuminate a metal whose work function is 0.5 eV. The ratio of the maximum speeds of the emitted electrons
View SolutionLights of two different frequencies whose photons have energies 1 eV and 2.5 eV respectively illuminate successively a metal surface whose work function is 0.7 eV. The ratio of the maximum speeds of the emitted electrons will have
View SolutionLight of two different frequencies whose photons have energies 1eV and 2.5 eV respectively illuminate a metallic surface whose work function is 0.5 eV successively. Ratio of maximum kinetic energy of emitted electrons will be:
View SolutionLights of two different frequencies whose photons have energies 1 and 2.5 eV, respectively, successively illuminate a metal whose work function is 0.5 eV. The ratio of the maximum speeds of the emitted electrons
View SolutionLight of two different frequencies whose photons have energies 1eV and 2.5 eV respectively illuminate a metallic surface whose work function is 0.5 eV successively. Ratio of maximum kinetic energy of emitted electrons will be:
View SolutionLight of two different frequencies whose photons have energies 1eV and 2.5 eV respectively illuminate a metallic surface whose work function is 0.5 eV successively. Ratio of maximum kinetic energy of emitted electrons will be:
View SolutionLight of two different frequencies whose photons have energies 1 eV and 2.5 eV respectively, successively illuminate a metallic surface whose work function is 0.5 eV. Ratio of maximum speeds of emitted electrons will be
View Solution

