The ratio of the dimensions of Planck constant and that of moment of inertia has the dimensions ofSolution in Kannada
frequency
velocity
time
angular momentum
The correct Answer is:A
As planck constnt (h) = energy frequency
and moment of inertia (I)=mass×(radius of gyration )2
∴[h]=[ML2T−2][T−1]=[ML2T−1]
and [I]=[M][L2]=[ML2T0]
Their corresponding ratio is
[h][I]=[ML2T−1][ML2T0]=[T−1]= [frequency ]
Topper's Solved these Questions
Similar Questions
A solenoid length 0.4cm, radius 1 cm and 400 turns of wire. If a current of 5 A is passed through this solenoid, what is the magnetic field inside the solenoid ?
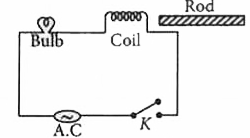
View SolutionIn the A. C. circuit shown, keeping 'K' pressed, if an iron rod is inserted into the coil, the bulb in the circuit
View SolutionPlanck constant has the same dimensions as
View SolutionThe ratio of the dimensions of plank's constant and that of the moment of inertia is the dimension of
View SolutionPlancks' constant has the dimensions of
View SolutionThe ratio of the dimension of Planck's constant and that of moment of inertia is the dimension of
View SolutionThe ratio of the dimensions of Planck's constant and that of moment of inertia has the dimensions of
View Solutionप्लांक नियतांक की विमा और जड़त्व आघूर्ण की विमा का अनुपात, एक विमा है -
View SolutionThe ratio of the dimension of planck constant and that of moment of inertia is the dimension of ……….
View SolutionThe ratio of the dimension of planck constant and that of moment of inertia is the dimension of ……….
View SolutionThe ratio of the dimensions of Planck constant and that of moment of inertia has the dimensions of
View SolutionThe ratio of the dimension of Planck's constant and that of the moment of inertia is the dimension of :
View SolutionThe ratio of the dimension of Planck's constant and that of moment of inertia is the dimension of
View SolutionThe ratio of the dimension of Planck's constant and that of the moment of inertia is the dimension of :
View SolutionThe ratio of the dimensions of plank's constant and that of the moment of inertia is the dimension of
View Solution

