The half life of a radioactive substance is 20 minutes. The time taken between 50% decay and 87.5% decay of the substance will be Solution in Kannada
40 minutes
10 minutes
30 minutes
25 minutes
The correct Answer is:A
Let in time of the substance decay and in time of the substance decay .
Then in time of the substance left undecayed and in time of the substance left undecayed .
According to radioactive decay law
where is the decay constant .
or
and
Dividing eqn . (ii) by eqn . (i) , we get
or
Here,
minutes
(20 minutes ) = 40 minutes
Topper's Solved these Questions
Similar Questions
A solenoid length 0.4cm, radius 1 cm and 400 turns of wire. If a current of 5 A is passed through this solenoid, what is the magnetic field inside the solenoid ?
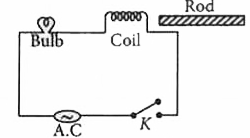
View SolutionIn the A. C. circuit shown, keeping 'K' pressed, if an iron rod is inserted into the coil, the bulb in the circuit
View SolutionThe half-life of a radioactive substance is 30 minutes, The time (in minutes) taken between 40 % decay and 85 % decay of the same radioactive substance is.
View SolutionThe half-life of a radioactive element is 100 minutes . The time interval between the stage to 50% and 87.5% decay will be:
View Solutionकिसी रेडयोएक्टिवे पदार्थ की अर्द्ध - आयु 30 मिनट है इसी रेडियोएक्टिव पदार्थ में 40% क्षय से 85% तक क्षय होने में लगा समय ( मिनटों में ) होगा :
View SolutionThe half-life of a radioactive substance is 20 min. the time taken between 50% decay and 87.5% decay of the substane will be
View SolutionHalf-life of a radioactive substance is 18 minutes. The time interval between its 20% decay and 80% decay in minutes is
View SolutionThe half life of a radioactive substance is 20 minutes, The time taken between 50% decay and 87.5% decay of the substance will be
View Solutionकिसी पदार्थ की अर्ध - आयु 20 मिनट है। 33% क्षय और 67% क्षय के बीच कितना समय अन्तराल है ?
View SolutionThe half-life of a radioactive substance is 20 minutes. The time taken between 50% decay and 87.5% decay of the substance will be
View SolutionHalf-life of a radioactive substance is 20 minutes. The time between 20% and 80% decay will be
View Solutionयदि दिये गये पदार्थ का 40 मिनट में 87.5% क्षय होता है, तो रेडियोधर्मी पदार्थ की अर्द्ध आयु होगी
View SolutionThe half-life of a radio active substance is 20 minutes. Of substance 50% From 87.5% Decay time
View SolutionHalf-life of a radioactive substance is 20 minute. The time between 20% and 80% decay will be
View SolutionCalculate the time interval between 33% decay and 67% decay if half-life of a substance is 20 minutes.
View Solution
