रदरफोर्ड सोडी का रेडियोएक्टिव विघटन नियम लिखिए तथा क्षय समीकरण प्राप्त कीजिए। अर्ध आयु एवं माध्य आयु में संबंध लिखिए।
रदरफोर्ड सोडी का रेडियो एक्टिव नियम- रदफोर्ड और सोडी ने रेडियो एक्टिव पदार्थों के लिए रेडियो क्षय का प्रयोगात्मक अधययन किया। अध्ययन के बाद निम्न नियम प्रतिपादित किया जिसे क्षय नियत कहते हैं। इस नियम के अनुसार-
1.रेडियोएक्टिव परमाणु के विघटन पर पदार्थ रासायनिक क्रिया इत्यादि का कोइ प्रभाव नहीं पड़ता। विघटन पूर्णतः स्वतः होता है। विघटन की घटना यादृच्छिक घटना होती है (अर्थात यह नही कहा जा सकता होगा) रेडियो एक्टिवता परमाणु के नाभिक का गुण होता है।
2.चरघातांकी क्षय का नियम- किसी भी रेडियोएक्टिव आसोटोप की निश्चित मात्रा में प्रति सेकण्ड विघटन होने वाले परमाणुओं की संख्या उस समय पर उपस्थित कुल सक्रिय परमाणुओं की संख्या पर निर्भर करती है। किसी समय विघटन की दर उस समय उपस्थित रेडियोएक्टिव नाभिकों की संख्या के अनुक्रमानुपाती होती है। इसे चारघातांकी क्षय का नियम कहते हैं।
क्षय समीकरण- माना किसी दिये गये नमूने में प्रारंभ में t=0 पर कुल सक्रिय परमाणुओं की संख्या N0, समय t पर सक्रिय परमाणुओं की संख्या N तथा समय (t+dt) पर (N−dN) है अर्थात dt समय में dN परमाणु विघटित होते हैं तो
परमाणुओं के विघटन की दर =−(dNdt)
प्रायिकता के नियम से −(dNdt)∝N
या dNN=−λN…………..1
यहां λ एक स्थिरांक है जिसे क्षयांक या विघटन स्थि)रांक कहते हैं।
समी 1 को व्यवस्थित करने पर
dNN=−λdt…….2
समी 2 का समाकलन करने पर
∫dNN=−∫λdt
∴logeN=−λt+C….3
जहां C एक नियतांक है C एक नियतांक है C का मान प्रारंभिक अवस्था से ज्ञात किया जाता है।
t=0 पर N=N0
अतः समीकरण 3 से
logeN0=0+C
या C=logeN0……..4
समी 4 का मान समी 3 में रखने पर
logeN=−λt+logeN0
या loge−logeN0=−λt
∴loge(NN0)=−λt तथा (NN0)−e−λt…5
या N=N0e−λt…..6
समीकरण 6 को रेडियो एक्टिव क्षयता का नियम या विघटन का नियम या चारघातांकी क्षय का नियम कहते हैं। इस नियम के अनुसार रेडियोएक्टिव परमाणु का विघटन चरघातांकी रूप में होता है । चरघातांकी क्षय को चित्र में प्रदर्शित किया गया है।
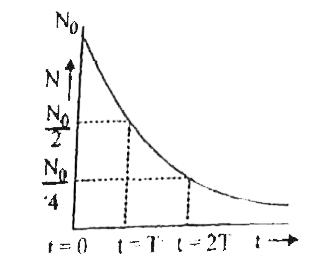
अर्द्ध आयु तथा माध्य आयु में संबंध
अर्ध आयु T1/2=0.693λ
औसत आयु का माध्य आयु T0=1λ
∴T1/2=0.693×1λ=0.693×T0
या T0=0.693T1/2
अतः माध्य आयु T0=0.693अर्द्धआयु(T1/2)
Topper's Solved these Questions
- BOOK - TRIPUTI PUBLICATIONCHAPTER - परमाणवीय एवं नाभिकीय भौतिकीEXERCISE - आंकिक प्रश्न6videos
परमाणवीय एवं नाभिकीय भौतिकी
- BOOK - TRIPUTI PUBLICATIONCHAPTER - परमाणवीय एवं नाभिकीय भौतिकीEXERCISE - लघूत्तरात्मक प्रश्न11videos
परमाणवीय एवं नाभिकीय भौतिकी
- BOOK - TRIPUTI PUBLICATIONCHAPTER - धारा वैद्युतिकी EXERCISE - आंकिक प्रश्न9videos
धारा वैद्युतिकी
- BOOK - TRIPUTI PUBLICATIONCHAPTER - प्रकाश विधुत प्रभाव एवं द्रव्य तरंगे EXERCISE - एकांकी प्रश्न8videos
प्रकाश विधुत प्रभाव एवं द्रव्य तरंगे
Similar Questions
.146C की अर्धआयु 5700 वर्ष है। इसका क्या अर्थ हैं?
View Solutionबोर मॉडल की दो सीमाएं लिखिए।
01:45View Solutionविद्युत वाहक बल तथा 2Ω आन्तरिक प्रतिरोध की एक बैटरी किसी प्रतिरोधक से संयोजित है | इसमें 0.5 A की विद्युत धारा प्रवाहित रही है तो प्रतिरोध ज्ञात कीजिए | यदि परिपथ बन्द है तो सैल की टर्मिनल वोल्टता क्या होगी |
04:45View Solutionसीजियम धातु के लिए देहली आवृत्ति 5.16×10−14Hz है । इसका कार्य फलन eV में ज्ञात कीजिए ।
View Solutionनिम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर लगभग 120 शब्दों में लिखिए
सचदेव बाबू का चरित्र-चित्रण कीजिएView Solutionसमीकरण निकाय को हल करने का क्रेमर नियम लिखिए
View Solutionपिता एवं पुत्र की आयु का योग 45 वर्ष है। चार वर्ष पूर्ण दोनों की आयु का गुणनफल 160 है। उनकी वर्तमान आयु ज्ञात कीजिए।
View Solutionनिम्नलिखित प्रश्न का उत्तर संक्षेप में लिखिए:
खीरा काटने में नवाब साहब की विशेषज्ञता का चित्रण अपने शब्दों में कीजिए।View Solutionकन्यादान' कविता का संदेश संक्षेप में लिखिए।
View Solutionनिम्नलिखित समस्त पदों का विग्रह कीजिए तथा समास के नाम लिखिए- नवरात्रि, चिंतामग्न
52:37View Solutionनिम्नलिखित समस्त पदों का विग्रह कीजिए तथा समास का नाम लिखिए-
उच्चाकांक्षा42:58View Solutionनिम्नलिखित समस्त पदों का विग्रह कीजिए तथा समास का नाम लिखिए- लोकप्रिय
01:20:00View Solutionतोप'कविता का प्रतिपाद्य अपने शब्दों में लिखिए।
01:05:33View Solutionरेडियोएक्टिव विघटन का नियम|माध्य आयु तथा अर्ध आयु
02:13View Solution12वी प्री बोर्ड स्पेशल |रेडियो नाभिक की अर्ध आयु
01:32View Solutionएन्ट्रॉपी तथा ऊष्मागतिकी का द्वितीय एवं तृतीय नियम तथा प्रशनोत्री
03:46View Solution
