प्रकाश किरणों के अपवर्तन को परिभाषित कीजिए। दो माध्यमों को पृथक करने वाले किसी गोलीय पृष्ठ पर अपवर्तन के लिये किरण चित्र बनाइए।
किसी गोलीय पृष्ठ पर अपवर्तन हेतु बिम्ब दूरी (u) प्रतिबिम्ब दूरी (v) माध्यम के अपवर्तनांक (n1,n2) तथा वक्रता त्रिज्या (R) में सम्बन्ध n2v−n1u=n2−n1R की व्युत्पत्ति कीजिए।
प्रकाश किरणों का अपवर्तन
किसी समांगी एवं पारदर्शी माध्यम में प्रकाश की किरणे सीधी रेखाओं में एक ही चाल से चलती है। लेकिन जब प्रकाश की किरण एक पारदर्शी माध्यम से दुसरे पारदर्शी माध्यम में तिर्यक आपतित होकर संचरण करती है तो दोनों माध्यमों को पृथक करने वाले पृष्ठ पर इसके संचरण की दिशा प्रारंभिक दिशा में विचलित हो जाती है इस परिघटना को प्रकाश का अपवर्तन कहते है।
गोलीय पृष्ठ पर अपवर्तन
माना SPS. एक गोलीय अवतल पृष्ठ है जो दो माध्यमों वायु तथा कांच को पृथक करता है इस पृष्ठ का ध्रुव P है तथा वक्रता केंद्र C है
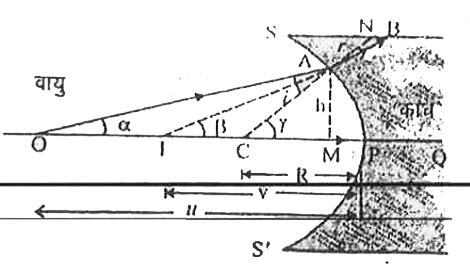
इसकी अक्ष PC पर एक बिन्दु वास्तु O रखी है O से एक आपतित किरण OA, पृष्ठ के बिन्दु A पर गिरती है। जहाँ CAN अभिलम्ब है अपवर्तन के नियमानुसार अपवर्तित किरण AB अभिलम्ब की ओर झुक जाती है दूसरी आपतित किरण OP, पृष्ठ पर अभिलम्बवत गिरती है अतः सीधी चली जाती है ये दोनों अपवर्तित किरणे AB तथा पीछे बढ़ाने पर बिन्दु I पर मिलती है
मान लो कि आपतन कोण ∠OAC=∠i,
अपवर्तन कोण
∠BAN=∠r,PQ=u,PI=−v,PC=−R
सही दूरियाँ आपतित प्रकाश किरण की दिशा के विपरीत नापी गई है इसलिए ऋणात्मक है माना कि OA,IA तथा CA मुख्य अक्ष से क्रमशः कोण α,β,γ बनाती है तथा A से मुख्य अक्ष पर खींचे गए अभिलम्ब की ऊँचाई h है।
ΔOCA में γ=α+i
i=γ−α . . .(1)
ΔICA में γ=β+r
r=γ−β . . . (2)
स्नैल के नियमानुसार η=sinisinr
जहाँ η दुसरे माध्यम काँचका पहले माध्यम हवा के सापेक्ष अववर्तनांक है
यदि गोलीय पृष्ठ का व्यास छोटा हो, तो बिन्दु A घ्रुव P के समीप होगा। तब कोण i तथा r छोटे होंगे। यदि i व r रेडियां में नापे जाये तो
sini=i तथा sinr=r
∵ir=η⇒i=ηr
इसमें समी . (1) व (2) से i व r के मान रखने पर -
(γ−α)=η(γ−β)
अथवा ηβ−α=(η−1)γ . . . . (3)
चूंकि पृष्ठ का व्यास छोटा माना गया है अतः कोण α,β,γ भी छोटे होंगे तथा बिन्दु A और M. ध्रुव P समीप होंगे। अतः
α=tanαAMMO=AMPO=h−u
β=tanβ=AMMI=AMPI=h−v
γ=tanγ=AMMC=AMPC=h−R
ये मान समीकरण (3) में रखने पर -
ηh−v−h−u=(η−1)h−R
ηv−1u=(η−1)R
∵ η=η2η1
∵η2η1v−1u=η2η1−1R
⇒η2v−η1v=η2−η1R . . . (4)
समीकरण (4) से हमें बिम्ब तथा प्रतिबिम्ब के बीच में माध्यम के अपवर्तनांक तथा गोलीय वक्रीय पृष्ठ की वक्रता त्रिज्या के पदों के रूप में सम्बन्ध प्राप्त होता है समीकरण (4) किसी भी प्रकार के वक्रित गोलीय पृष्ठ के लिए मान्य है।
Topper's Solved these Questions
Similar Questions
एक छोटी दूरबीन के अभिदृश्यक तथा नेत्रिका की फोकस दूरियाँ क्रमशः 192 cm तथा 8cm है। इसकी आवर्धन क्षमता तथा दोनों लैंसों के बीच की दूरी ज्ञात कीजिए।
View Solutionपार्श्विक विस्थापन किसे कहते हैं ? किसी दर्पण की फोकस दूरी तथा वक्रता त्रिज्या में सम्बन्ध स्थापित कीजिए।
अथवा
अवतल दर्पण के लिये किरण चित्र बनाकर सिद्ध कीजिए कि दर्पण की फोकस दूरी उसकी वक्रता त्रिज्या की आधी होती है।
View Solutionउस भौतिक राशि का नाम लिखिए जिसका मात्रक जूल/कूलॉम है। बताइये कि यह राशि सदिश है या अदिश।
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View SolutionR1 तथा R2 वक्रता -त्रिज्यावाली दो सतहों से घिरे एक लेंस को चित्र के अनुरूप रखा गया है। सिद्ध करें की
n3v−n1u=n2−n1R1+n3−n2R
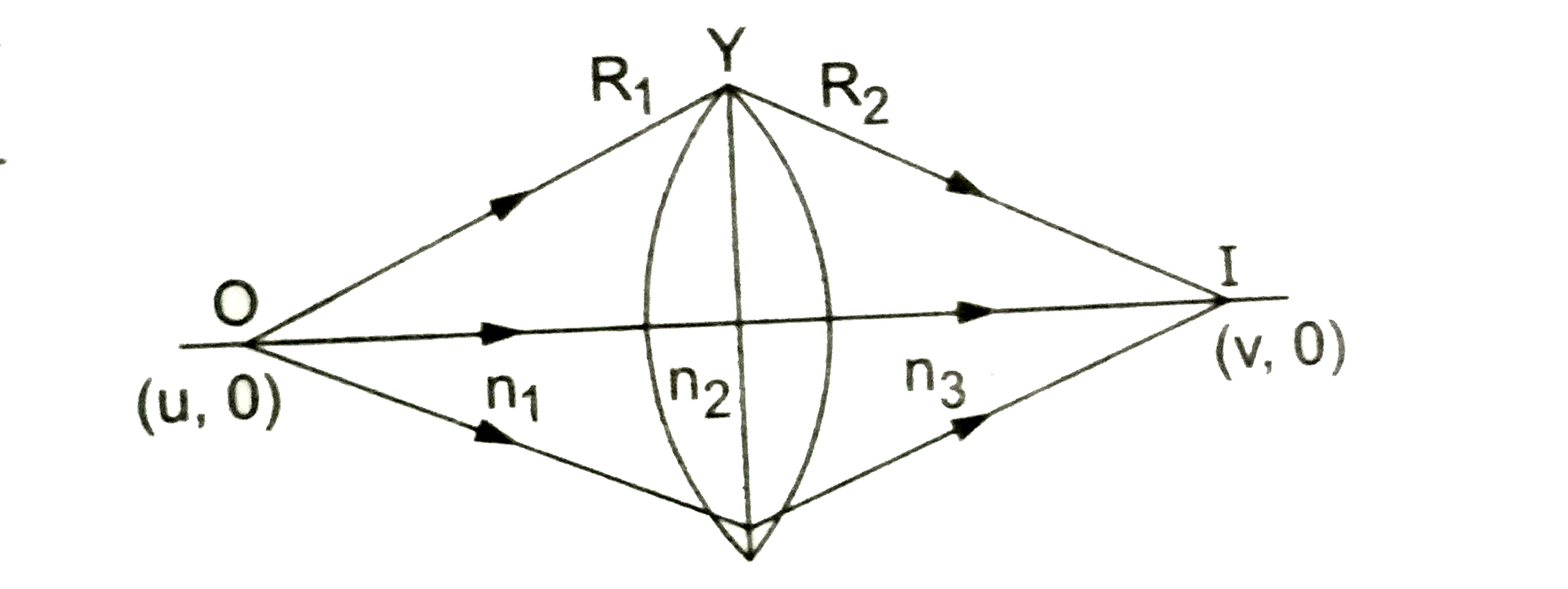
View Solutionu=v=w=1 के लिए, यदि n1n2l1l2=(a+bb+c), तब
View Solutionगोलीय पृष्ठ पर अपवर्तन
View SolutionExam special|प्रकाश - परावर्तन तथा अपवर्तन#!#प्रकाश के अपवर्तन के नियम #!#अपवर्तनांक
View SolutionExam special|प्रकाश - परावर्तन तथा अपवर्तन#!#गोलीय लेंसों के पद
View SolutionExam special|प्रकाश - परावर्तन तथा अपवर्तन#!#गोलीय लेंस से अपवर्तन
View SolutionObtain lens maker's formula using the expression n2v−n1u=n2−n1R, propagating from a rarer medium of refractive index (n1) to a denser medium of refractive index (n2) is incident on the convex side of spherical refracting surface of radius of curvature R.
View SolutionBoard special|प्रकाश - परावर्तन तथा अपवर्तन#!#अपवर्तन के नियम #!#ममध्यम का अपवर्तनांक
View Solutionगोलीय प्रिसठ पर अपवर्तन
View Solutionगोलीय प्रस्थ पर अपवर्तन
View Solutionगोलीय पृष्ट पर अपवर्तन
View Solutionगोलीय प्रस्थ पर अपवर्तन
View Solution
