If D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
centroid of the triangle DEF is the same as that of ABC
orthocenter of the triangle DEF is the circumcentre of ABC
orthocenter of the triangle DEF is the incenter of ABC
centroid of the triangle DEF is not the same as that of ABC
The correct Answer is:A, B
Let D, E and F be the mid-point of the sides of ΔABC.
E and F are mid-point of AC and AB, respectively

So, EF∣∣BCandEF=12BC
Thus, AD will also divide EF into equal parts.
Hence, DH is also median of ΔDEF
Similarly BE, median of ΔABC, is also median of ΔDEF.
These two lines meet at G.So the centroids of both triangles are same.
The orthocenter, O of ΔDEF is the point of intersection of the perpendiculars DH and EK drawn from D and E, respectively.

Since, EF∣∣BC, DH is perpendicular to BC also.
Similarly EK is perpendicular to AC.
So, orthocenter of ΔDEF and circumcentre of ΔABC is the same points
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Comprehension)
Explore 34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Matrix)
Explore 6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Single)
Explore 80 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OAAA. a zero vectorBB. a unit vectorCC. 0DD. none of theseIn the given figure, D, E and F are the midpoints of the sides BC, CA and AB of ΔABC.BE bisect DF at X while CF bisect DE at Y, then BC = a XY. Find a.
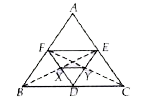 A3B4C2D1/4
A3B4C2D1/4
Let D,EandF be the middle points of the sides BC,CAandAB, respectively of a triangle ABC. Then prove that →AD+→BE+→CF=→0 .
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionIf D,E,andF are three points on the sides BC,AC,andAB of a triangle ABC such that AD,BE,andCF are concurrent, then show that BD⋅CE⋅AF=DC⋅EA⋅FB .
View SolutionIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
View Solution

