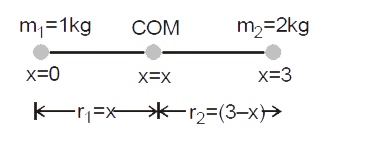Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
Since , both the particles lie on x - axis , the CM will also lie on x- axis . Let the CM be located at x = x, then
(m1+m2)x=m1x1+m2x2 ⇒(1+2)x=1×1+2×3⇒x=2.3m
Thus , the CM of the two masses and at located at x = 2.33 m from origin .
(i.e) between the two masses and at 1.33 m distance from the 1 kg mass .
Alternate Method : Let CM be at r1 distance from m1
d=x2−x1=3−1=2m
r1=(m2m2+m1)=(22+1)×2=1.33m
Thus the CM lies at 1.33 m fron the 1 kg mass .
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 1
Explore 9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 4
Explore 11 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
Knowledge Check
Two partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in kg−m2)
A6B9C8D12Two objects of masses 1kg and 2kg separated by a distance of 1.2m are rotating about their centre of mass. Find the moment of inertia of the system
A0.96kgm2B0.48kgm2C0.83kgm2D0.72kgm2Two particle of masses 4kg and 8kg are kept at x=−2m and x=4m respectivley. Then, the gravitational field intensity at the origin is
AGB2GCG/2DG/4
Two particles of masses 1kg and 2kg are placed at a distance of 50cm. Find the initial acceleration of the first particle due to gravitational force.
View SolutionCentre of mass of two particles with masses 1kg and 2kg located at (2,0,2) and (1,1,0) has the co-ordinates of ?
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionThe coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
View SolutionThree particles of masses 1kg,32kg,and2kg are located at the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
View Solution