Two particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.

Since, both the particles lie on x-axis, the COM will also lie on x-axis. Let the COM is located at x = x, then
r1 = distance of COM from the particle of mass 1 kg = x and r2 = distance of COM from the particle of mass 2 kg = (3 – x)
Using r1r2=m2m1
or x3−x=21
thus, the COM of the two particles is located at x = 2m.
Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 1
Explore 71 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
Two particle of mass 4 kg & 2kg are located as shown in figure then find out the position of centre of mass.
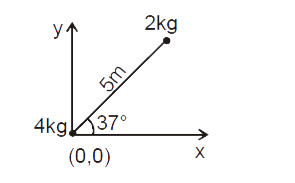
View SolutionThe coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
View Solution
Knowledge Check
Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
A2m from 1 kgB2m from 2 kgC1m from 1 kgDnone of theseTwo partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in kg−m2)
A6B9C8D12Two objects of masses 1kg and 2kg separated by a distance of 1.2m are rotating about their centre of mass. Find the moment of inertia of the system
A0.96kgm2B0.48kgm2C0.83kgm2D0.72kgm2
Two particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only foces acting on the particles are their mutual gravitation find the initial acceleration of hthe two particles.
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionParticles of masses 1kg and 3kg are at 2i+5j+13k)m and (−6i+4j−2k)m then instantaneous position of their centre of mass is
View SolutionA rigid body consists of a 3kg mass located at →r1=(2ˆi+5ˆj)m and a 2kg mass located at →r2=(4ˆi+2ˆj)m. The position of centre of mass is
View SolutionTwo particle of masses 4kg and 8kg are kept at x=−2m and x=4m respectivley. Then, the gravitational field intensity at the origin is
View Solution

