The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case I the mass m is lifted by attaching a mass $2 m$ to the other end of rope with a constant downward force $F = 2 m g$ , where g is acceleration due to gravity The acceleration of mass m in case I is
.

A

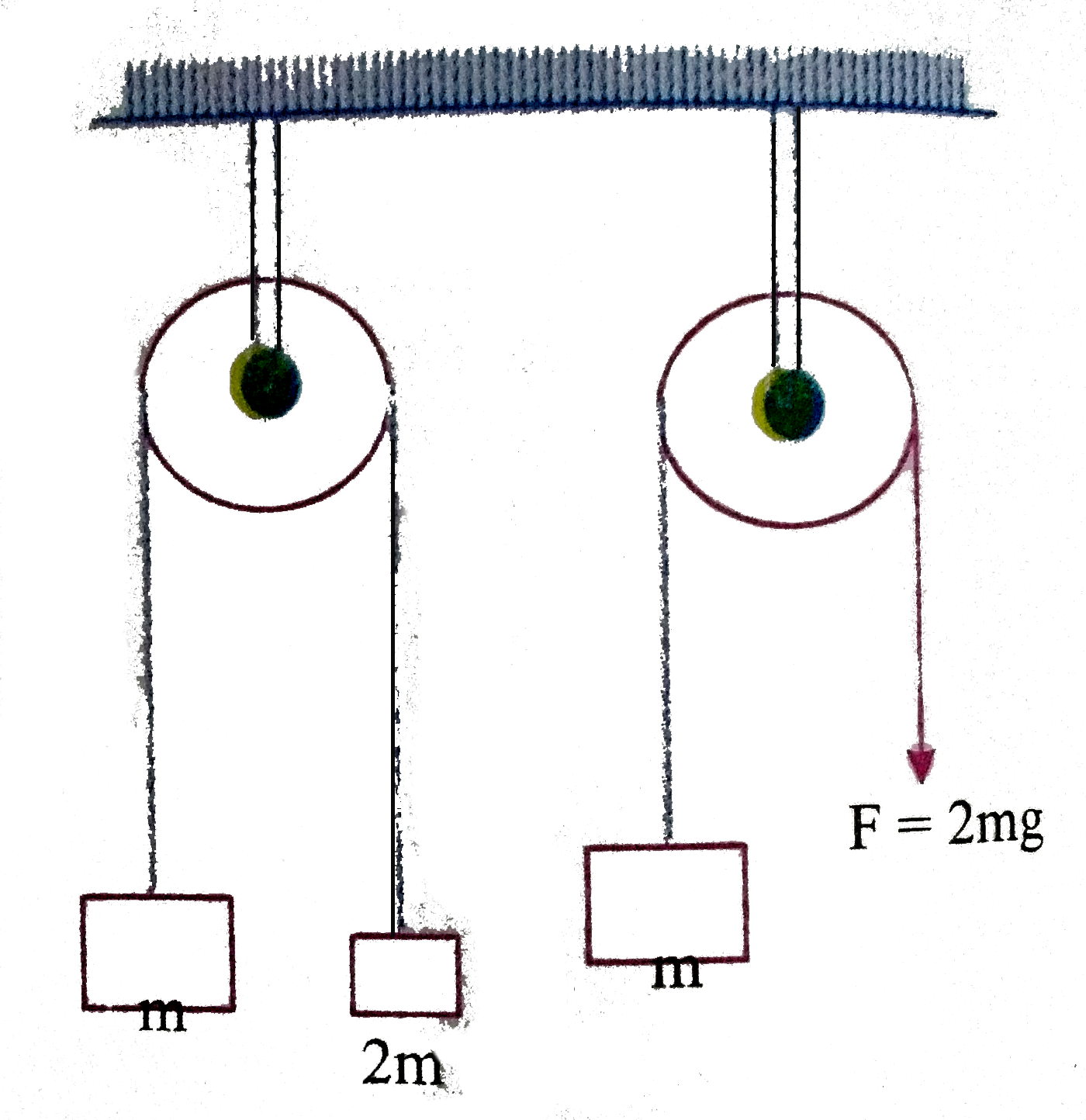Zero

B

More than that in case (b)

C

Less than that in case (b)

D

Equal to that is case (b)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

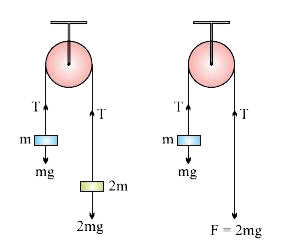
In case (a)
$T - m g = m A_{a} \dots(i)$
$2 m g - T = 2 m A_{a} \dots(ii)$
Add (i) & (ii)
$A_{a} = g / 3$
In case (b)
Tension in string $T_{b} = 2 m g$
$(∵ Tension in uniform at every points in ideal string)$
$\Rightarrow A_{b} = \frac{2 m g}{m} = 2 g \Rightarrow a_{b} > A_{a}$

Updated on:21/07/2023

|

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Figure shown two pulley arrangements for lifting a mass $m$ . In case-1, the mass is lifting by attaching a mass 2m while in case-2 the mass is lifted by pulling the other end with a downward force $F = 2 m g$ . If $a_{a}$ and $a_{b}$ are the accelerations of the two masses then (Assume string is massless and pulley is ideal).

A $a_{a} = a_{b}$
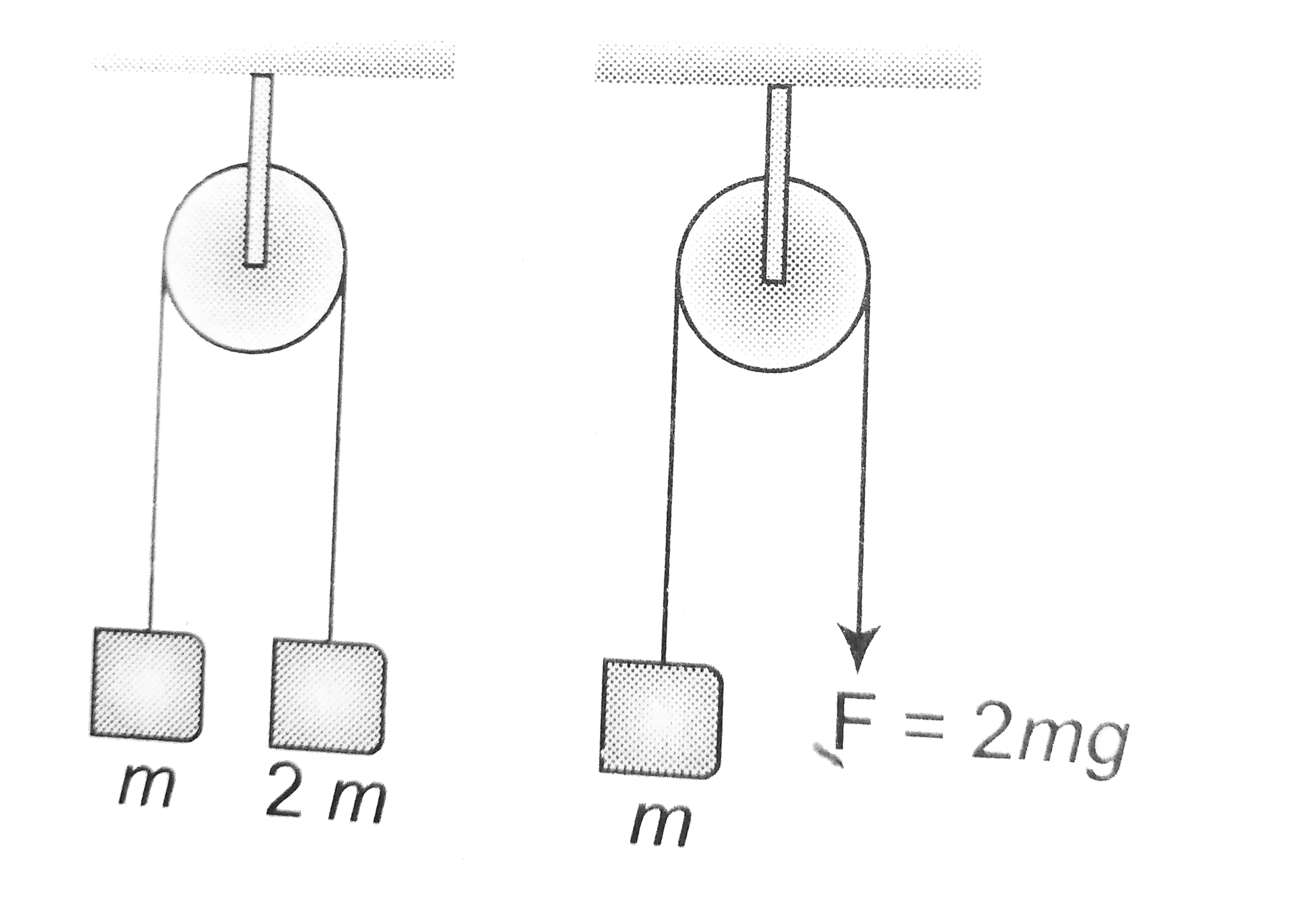B $a_{a} = \frac{a_{b}}{2}$
C $a_{a} = \frac{a_{b}}{3}$
D $a_{a} = 2 a_{b}$
In fig mass m is lifted up by attaching a mass 2m to the other end of the string while in fig
(b) m is lifted by pulling the other end of the string with a constant force $F = 2 m g$ then:

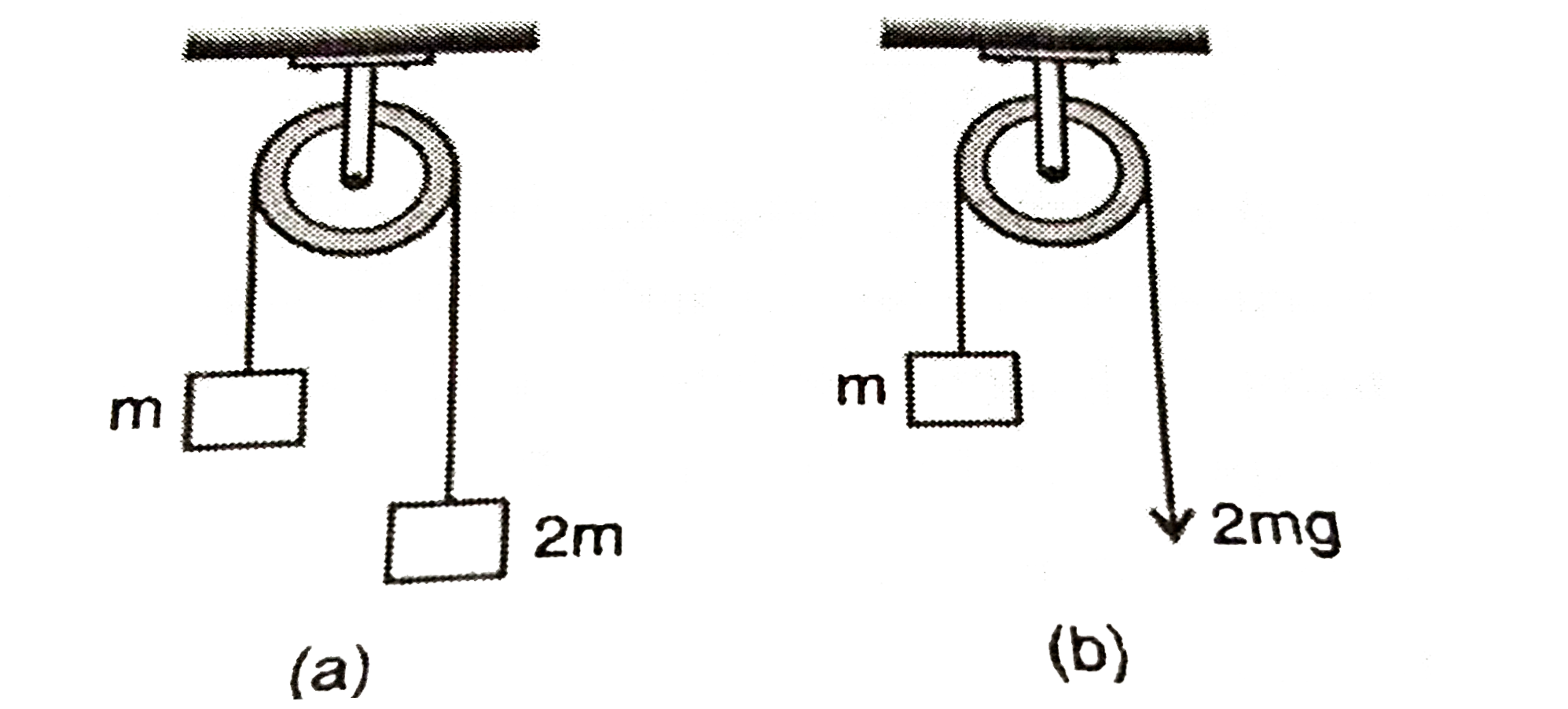Aacceleration of m in the two situations is same and non - zero
Bacceleration of m in situation
(a) is more than that of in situation(b)
Cacceleration of m in situation
(a) is less than that of in situation
(b)
Dacceleration of m in the two situations is same and equals to zero
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

A $g / 2$
B0
Cg
D3g

NARAYNA-LAW OF MOTION-EXERCISE - IV

Home
Ask Doubt
Profile