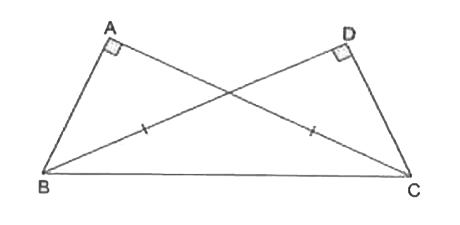
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD =∠CBD.
Since, ∠ABC and ∠ADC are 90.
These angles are in the semi-circle.
Thus, both the triangles are lying in the semi-circle and AC is the diameter of the circle.
Points A,B,C and D are concyclic.
Thus, CD is the chord.
Angles in the same segment of the circle are equal. Thus,
∠CAD=∠CBD
Topper's Solved these Questions
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.4
6 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.1
1 Videos
- CONSTRUCTIONSBOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.2
5 Videos
Similar Questions
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD =∠CBD.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View Solution△ABC AND △ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
View SolutionIn the given figure, triangles ABC and DCB are right angled at A and D respectively and AC = DB. Prove that △ABC=△DCB.
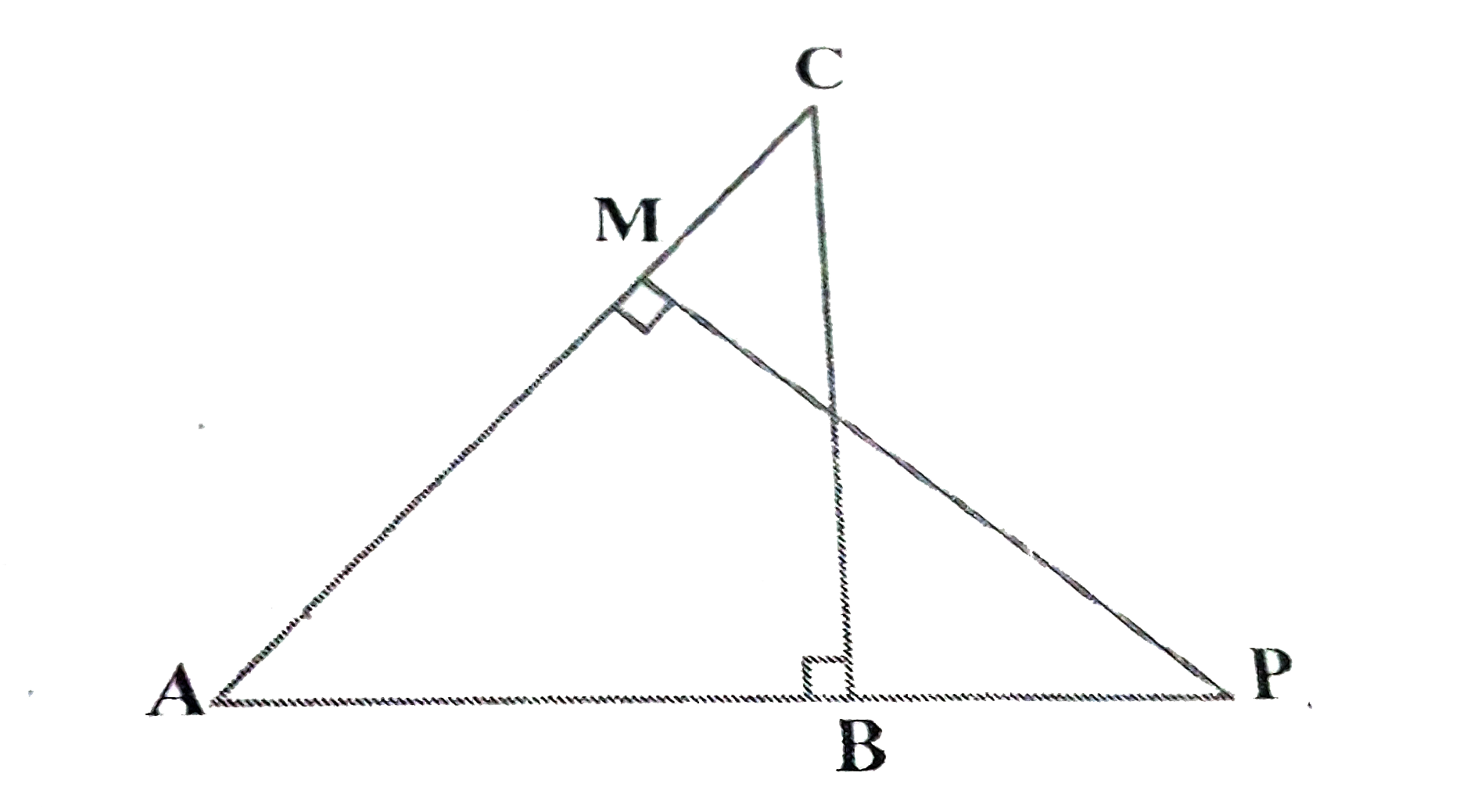
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
View SolutionABC and ADC are two equilateral triangles on a common base AC. Find the angles of the resulting quadrilateral. Show that it is a rhombus.
View SolutionABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View Solution. In right angled triangle ABC,∠A is right angle. AD is perpendicular to the hypotenuse BC. Prove that ΔABCΔACD=BC2AC2
View SolutionLet ABC be a right triangle with length of side AB=3 and hypotenuse AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View Solution
