ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70o,∠BAC is 30o, find ∠BCD. Further, if AB = BC, find∠ECD.
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Identify Given Angles:
- We have ∠DBC=70∘ and ∠BAC=30∘.
2. Find Angle ∠CAD:
- Since ABCD is a cyclic quadrilateral, the angles subtended by the same chord are equal. Therefore, we can say:
∠CDB=∠CAB
- Thus, ∠CAD=∠DBC=70∘.
3. Calculate Angle ∠BAD:
- The sum of angles in triangle ABC gives us:
∠BAD+∠BAC+∠CAD=180∘
- Substituting the known values:
∠BAD+30∘+70∘=180∘
- Simplifying this:
∠BAD+100∘=180∘
∠BAD=180∘−100∘=80∘
4. Use the Cyclic Quadrilateral Property:
- In cyclic quadrilateral ABCD, the sum of opposite angles is 180∘:
∠A+∠C=180∘
- We already found ∠A=∠BAD=80∘. Let ∠BCD=x:
80∘+x=180∘
- Therefore:
x=180∘−80∘=100∘
- Thus, ∠BCD=100∘.
5. Find Angle ∠ECD:
- Since AB=BC, triangle ABC is isosceles, which means ∠A=∠C.
- We already have ∠A=30∘, so ∠C=30∘.
- Now, in triangle BCD:
∠BCD+∠CDB+∠ECD=180∘
- Substituting the known values:
100∘+70∘+∠ECD=180∘
- Therefore:
∠ECD=180∘−170∘=10∘
Final Answers:
- ∠BCD=100∘
- ∠ECD=10∘
- We have ∠DBC=70∘ and ∠BAC=30∘.
- Since ABCD is a cyclic quadrilateral, the angles subtended by the same chord are equal. Therefore, we can say:
∠CDB=∠CAB
- Thus, ∠CAD=∠DBC=70∘.
- The sum of angles in triangle ABC gives us:
∠BAD+∠BAC+∠CAD=180∘
- Substituting the known values:
∠BAD+30∘+70∘=180∘
- Simplifying this:
∠BAD+100∘=180∘
∠BAD=180∘−100∘=80∘
- In cyclic quadrilateral ABCD, the sum of opposite angles is 180∘:
∠A+∠C=180∘
- We already found ∠A=∠BAD=80∘. Let ∠BCD=x:
80∘+x=180∘
- Therefore:
x=180∘−80∘=100∘
- Thus, ∠BCD=100∘.
- Since AB=BC, triangle ABC is isosceles, which means ∠A=∠C.
- We already have ∠A=30∘, so ∠C=30∘.
- Now, in triangle BCD:
∠BCD+∠CDB+∠ECD=180∘
- Substituting the known values:
100∘+70∘+∠ECD=180∘
- Therefore:
∠ECD=180∘−170∘=10∘
- ∠BCD=100∘
- ∠ECD=10∘
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘, then Cand∠D are
A100∘,130∘B115∘,115∘C110∘,120∘D130∘,100∘
ABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
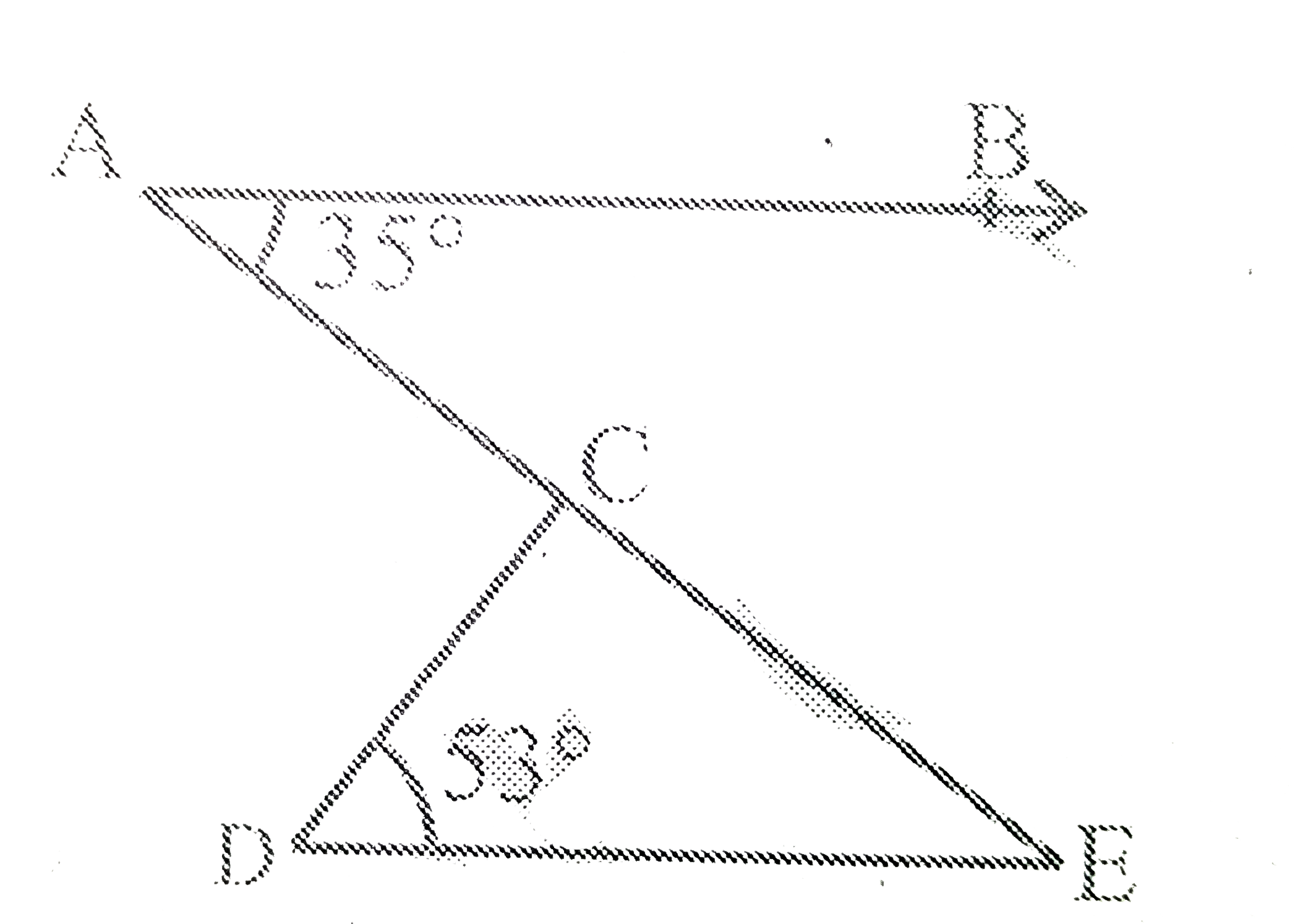 View Solution
View SolutionIn Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
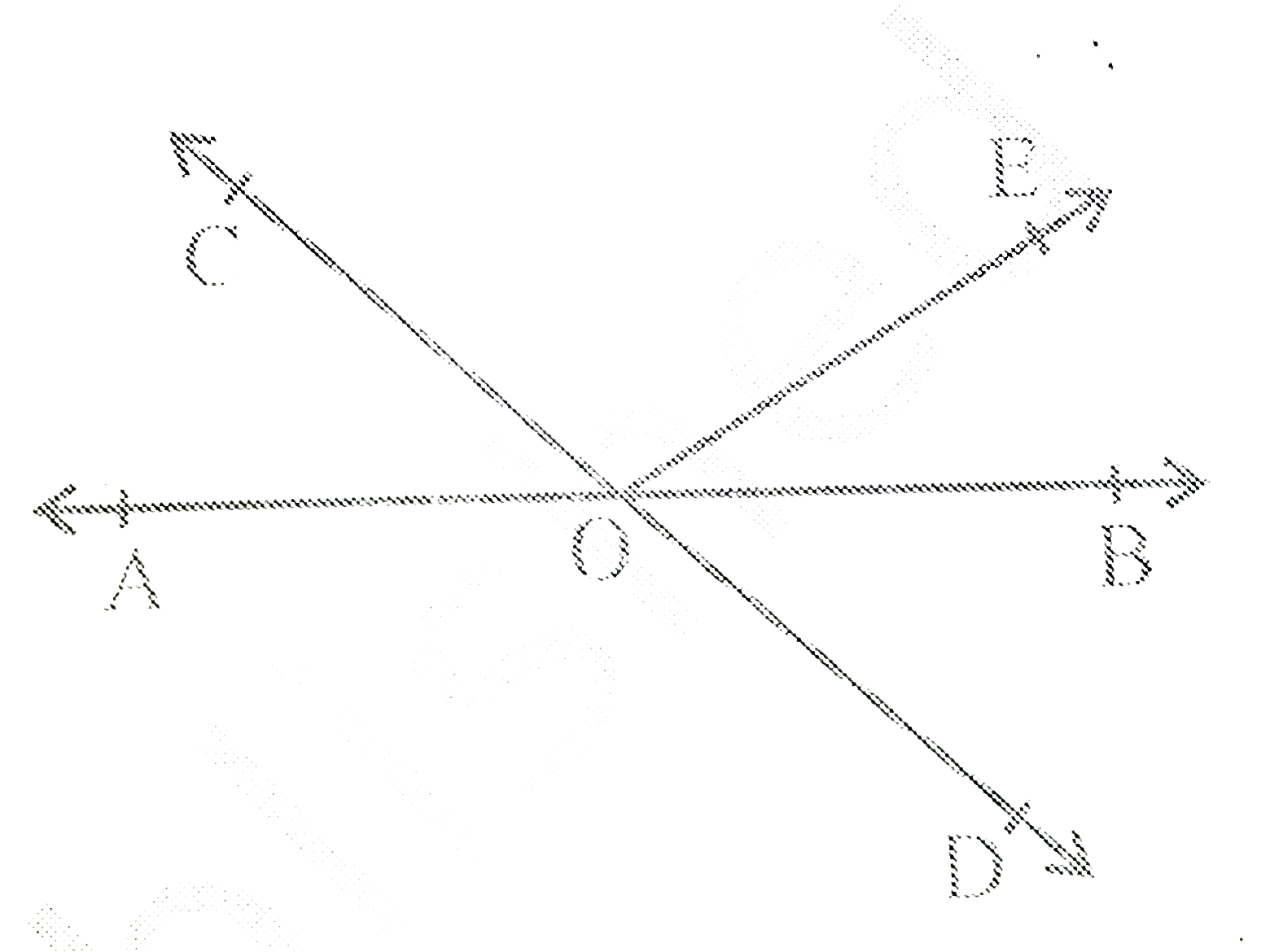 View Solution
View Solution

