Question

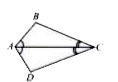
If the diagonal BD of a quadrillateral ABCD bisects both $\angle B\text{and}\angle D$. Prove that $\frac{AB}{BC}=\frac{AD}{CD}$.

Explanation

To prove that $$\frac{AB}{BC}=\frac{AD}{CD}$$ given that the diagonal $$BD$$ of quadrilateral $$ABCD$$ bisects both $$\angle B$$ and $$\angle D$$, we can use the Angle Bisector Theorem. Here’s a step-by-step solution:

Step 1: Understand the Given Information
We have a quadrilateral \(ABCD\) with diagonal \(BD\) that bisects \(\angle B\) and \(\angle D\).

Step 2: Apply the Angle Bisector Theorem at Vertex B
According to the Angle Bisector Theorem, if a point \(D\) lies on the angle bisector of \(\angle ABC\), then:
\( \frac{AB}{BC} = \frac{AD}{DC} \)
Let’s denote the intersection point of \(AC\) and \(BD\) as \(O\).

Step 3: Apply the Angle Bisector Theorem at Vertex D
Similarly, since \(BD\) also bisects \(\angle ADC\), we can apply the Angle Bisector Theorem again:
\( \frac{AD}{DC} = \frac{AO}{OC} \)

Step 4: Set Up the Equations
From Step 2, we have:
\( \frac{AB}{BC} = \frac{AO}{OC} \quad \text{(1)} \)
From Step 3, we have:
\( \frac{AD}{DC} = \frac{AO}{OC} \quad \text{(2)} \)

Step 5: Equate the Two Ratios
Since both equations (1) and (2) have the same right-hand side \(\frac{AO}{OC}\), we can equate the left-hand sides:
\( \frac{AB}{BC} = \frac{AD}{DC} \)

Step 6: Conclusion
Thus, we have proved that:
\( \frac{AB}{BC} = \frac{AD}{CD} \)