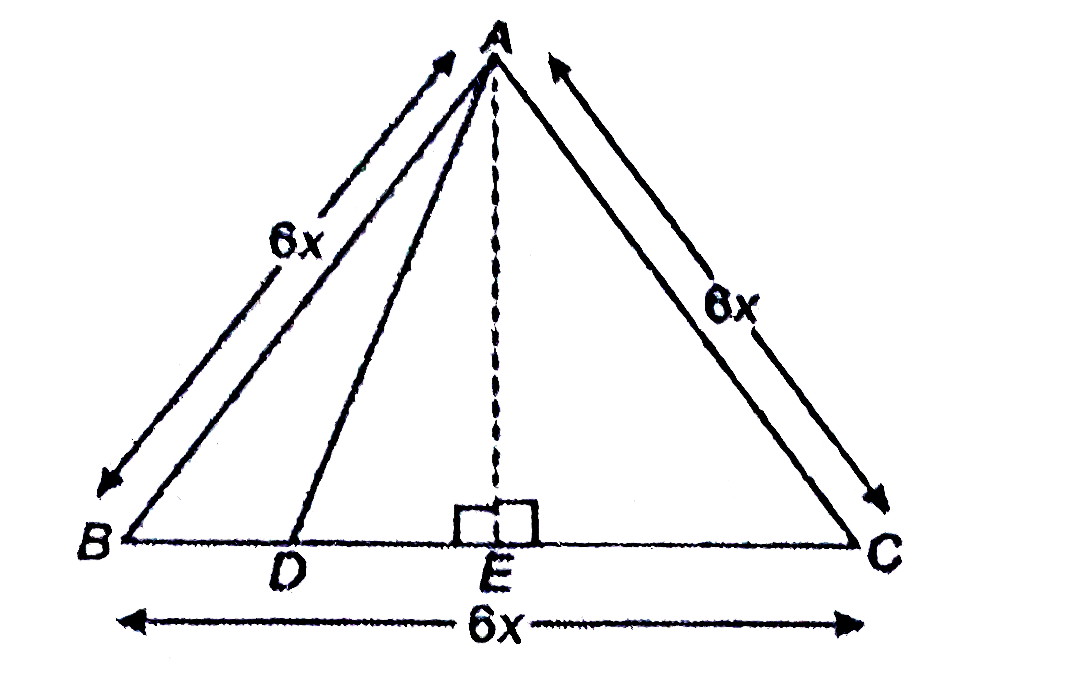
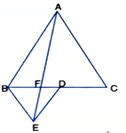
In an equilateral triangle ABC the side BC is trisected at D. Prove that 9 AD2=7 AB2
Video Solution
Text Solution
Let AB = BC = AC = 6x
Also BD=13BC=13×6x=2x
and BE=EC=BC2=3x
( perpendicular bisects the base in an equilatyeral triangle).
DE= BE- BD = 3x-2x=x
Now, by pythagoras theorem,
AB2=AE2+BE2=AD2−DE2+BE2
(6x2)=AD2−x2+(3x)2
⇒ AD2=36x2+x2−9x2=28x2
9AD2=9×28x2=9×7×4x2=7×36x2=7(AB)2
9AD2=7AB2
|
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In an equilateral triangle ABC, the side BC is trisected at D. Find the value of AD2 :
 A97AB2B79AB2C34AB2D45AB2
A97AB2B79AB2C34AB2D45AB2In an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2Dnone of theseIn an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2DNone of these
In an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)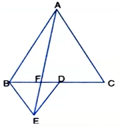
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View Solution
