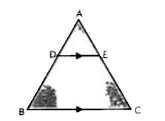
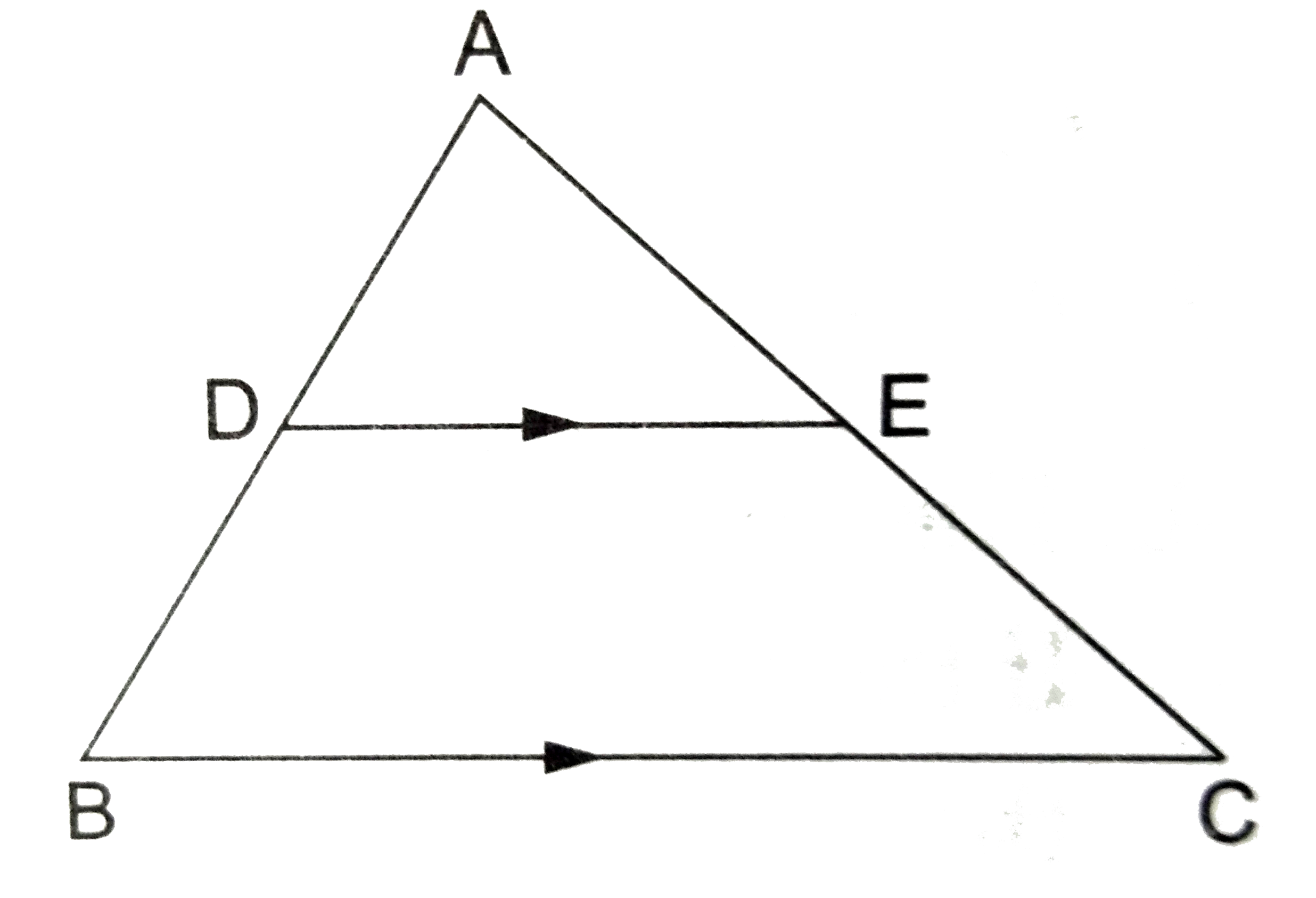
In figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
In △ADEand△ABC
∠1=∠2 ( corresponding angles as DE||BC)
∠A=∠A (common)
△ADE~△ABC (AA corollary)
ar(△ADE)ar(△ABC)=AD2AB2=DE2BC2=AE2AC2...(1)
ratio of areas of two similar triangles is equal to the ratio squares of their corresponding sides)
Now, ar(trapeziumBDEC)ar(△ADE)=54
⇒ ar(△ABC)−ar(△ADE)ar(△ADE)=54
ar(△ABC)ar(△ADE)−1=54⇒ar(△ABC)ar(△ADE)=94
⇒ ar(△ADE)ar(△ABC)=49 ....(2)
DE2BC2=49 [ from (1) and (2)]
DEBC=23
DE:BC= 2:3
Now from (1) and (2) , we get
ar(△ADE)ar(△ABC)=AD2AB2=49
ADAB=23⇒ADAD+BD=23
AD+BDAD=32⇒1+BDAD=32
BDAD=32−1=12
2AD=12⇒AD=4cm

Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
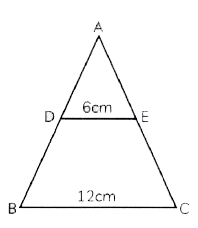
In the given figure, DE is parallel to BC and the ratio of the areas of ΔADE and trapezium BDEC is 4:5. What is DE: BC?
A1:2B2:3C4:5DNone of theseIn the adjacent figure DE is parallel to BC and ratio of areas of ΔADE and trapezium BDEC is 4 : 5. What is the value of DE : BC?
 A1:2B2:3C4:5DNone of these
A1:2B2:3C4:5DNone of theseIn figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
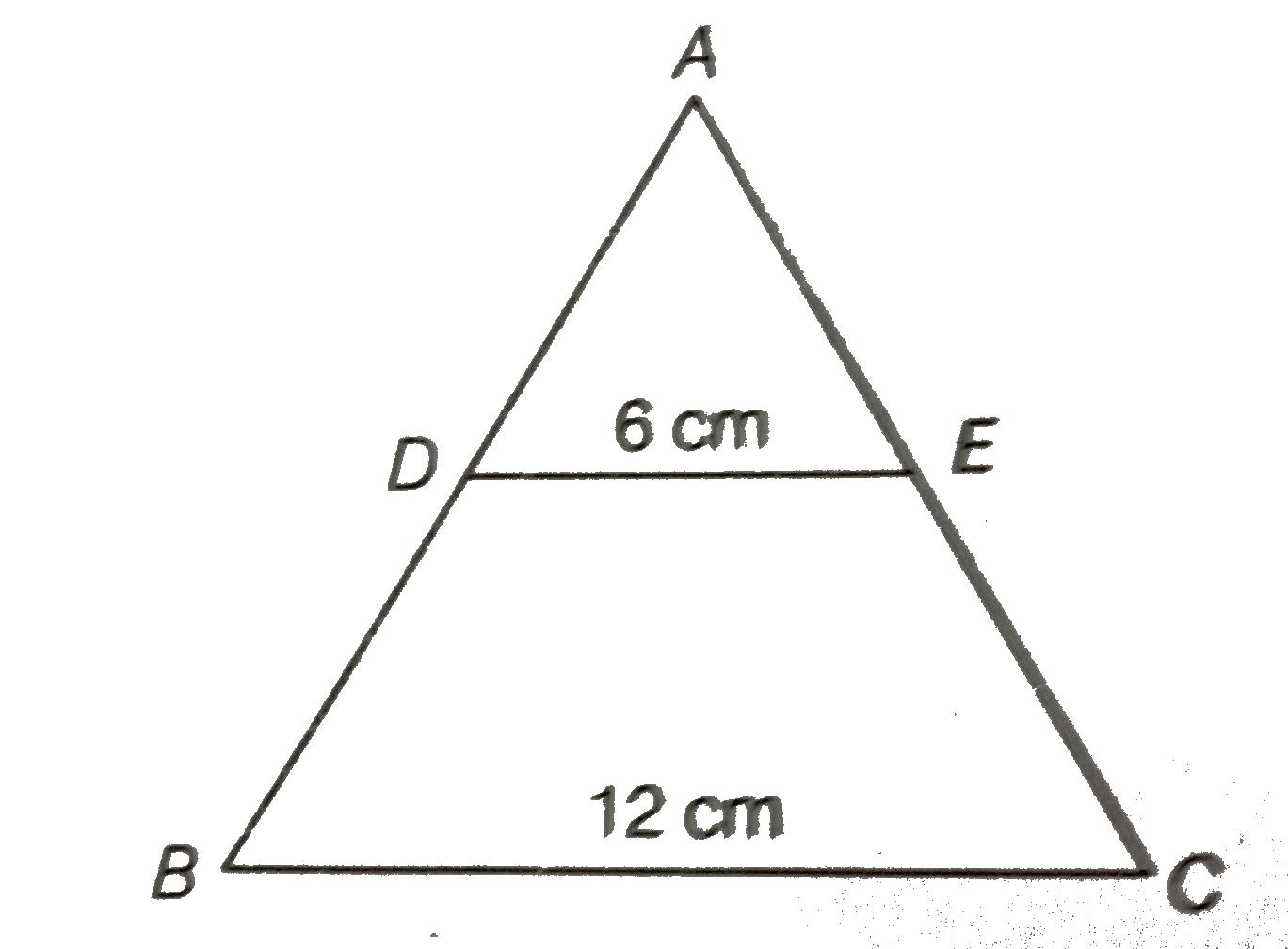 A1:3B1:2C2:5D3:5
A1:3B1:2C2:5D3:5
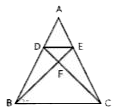
In the figure, if DE∣∣BCandAD:AB=5:9, then the ratio of areas of ΔDEFandΔBFC is
View SolutionIn the given figure, DE∣∣BCandDE:BC=3:5. Calculate the ratio of areas of ΔADE and the trpezium BCED.
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE||BC and AD/BD=3/4 . The ratio of the area of △ABC to the area of trapezium DECB is:
त्रिभुज ABC में, AB और AC भुजाओं पर 2 बिंदु क्रमशः D और E इस तरह है कि DE||BC और AD/BD=3/4 है| △ABC क्षेत्रफल का समलंब चतुर्भुज DECB के क्षेत्रफल से अनुपात है :
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =5/6 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =5/6 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल के बीच अनुपात ज्ञात करें |
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution