In a trapezium ABCD, O is the point of intesection of AC and BD, AB||CD and AB=2×CD. If the area of △AOB=84cm2 . Find the area of △COD.
42cm2
21cm2
25cm2
40cm2
The correct Answer is:B
To solve the problem step by step, we will use the properties of similar triangles and the relationship between their areas.
1. Identify the Given Information:
- In trapezium ABCD, AB || CD.
- AB = 2 * CD.
- Area of triangle AOB = 84 cm².
- We need to find the area of triangle COD.
2. Understanding the Similar Triangles:
- Since AB is parallel to CD, the angles formed by the intersection of the diagonals AC and BD create alternate angles.
- Therefore, we have:
- ∠AOB = ∠COD (alternate angles)
- ∠OAB = ∠OCD (alternate angles)
- This means that triangles AOB and COD are similar by the AA (Angle-Angle) criterion.
3. Setting Up the Ratio of Areas:
- For similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
- Let the length of CD be x. Then, the length of AB is 2x.
- The ratio of the lengths of AB to CD is:
ABCD=2xx=2
- The ratio of the areas of triangles AOB and COD is:
Area of △AOBArea of △COD=(ABCD)2=22=4
4. Using the Area of Triangle AOB:
- Let the area of triangle COD be denoted as A.
- From the ratio of the areas, we have:
84A=4
- Cross-multiplying gives:
84=4A
5. Solving for A:
- Dividing both sides by 4:
A=844=21 cm2
6. Conclusion:
- The area of triangle COD is 21 cm².
Final Answer:
The area of triangle COD is 21 cm².
- In trapezium ABCD, AB || CD.
- AB = 2 * CD.
- Area of triangle AOB = 84 cm².
- We need to find the area of triangle COD.
- Since AB is parallel to CD, the angles formed by the intersection of the diagonals AC and BD create alternate angles.
- Therefore, we have:
- ∠AOB = ∠COD (alternate angles)
- ∠OAB = ∠OCD (alternate angles)
- This means that triangles AOB and COD are similar by the AA (Angle-Angle) criterion.
- For similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
- Let the length of CD be x. Then, the length of AB is 2x.
- The ratio of the lengths of AB to CD is:
ABCD=2xx=2
- The ratio of the areas of triangles AOB and COD is:
Area of △AOBArea of △COD=(ABCD)2=22=4
- Let the area of triangle COD be denoted as A.
- From the ratio of the areas, we have:
84A=4
- Cross-multiplying gives:
84=4A
- Dividing both sides by 4:
A=844=21 cm2
- The area of triangle COD is 21 cm².
The area of triangle COD is 21 cm².
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
In trapezium ABCD, AB || CD and AB = 2 CD. Its diagonals intersect at O. If the area of ΔAOB=84cm2, then the area of ΔCOD is equal to
A72cm2B21cm2C42cm2D26cm2ABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 cm2 . What is the area of square ?
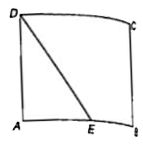 A400cm2B625cm2C729cm2D576cm2
A400cm2B625cm2C729cm2D576cm2ABCDis a trapezium, such that AB=CD and AD∣∣BC.AD=10cmandBC=18cm. If the area of ABCDis 70cm2, what is the value (in cm) of CD?
A5B√29C√41D6
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View SolutionIf ABCD is a trapezium, AB∣∣CD.AECD is a rhombus and E is the midpoint of AB and thearea of trape zium is 72cm2 then the area of ΔECD rhombus is
View SolutionABCD is a rectangle of perimeter 48 cm with AB = 6 cm and CD = DE .What is the area of the triangle ACE ?

View SolutionABCDis a trapezium, such that AB=CD and AD∣∣BC.AD=10cmandBC=18cm. If the area of ABCDis 70cm2, what is the value (in cm) of CD?
View SolutionIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :

View Solution

