In trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
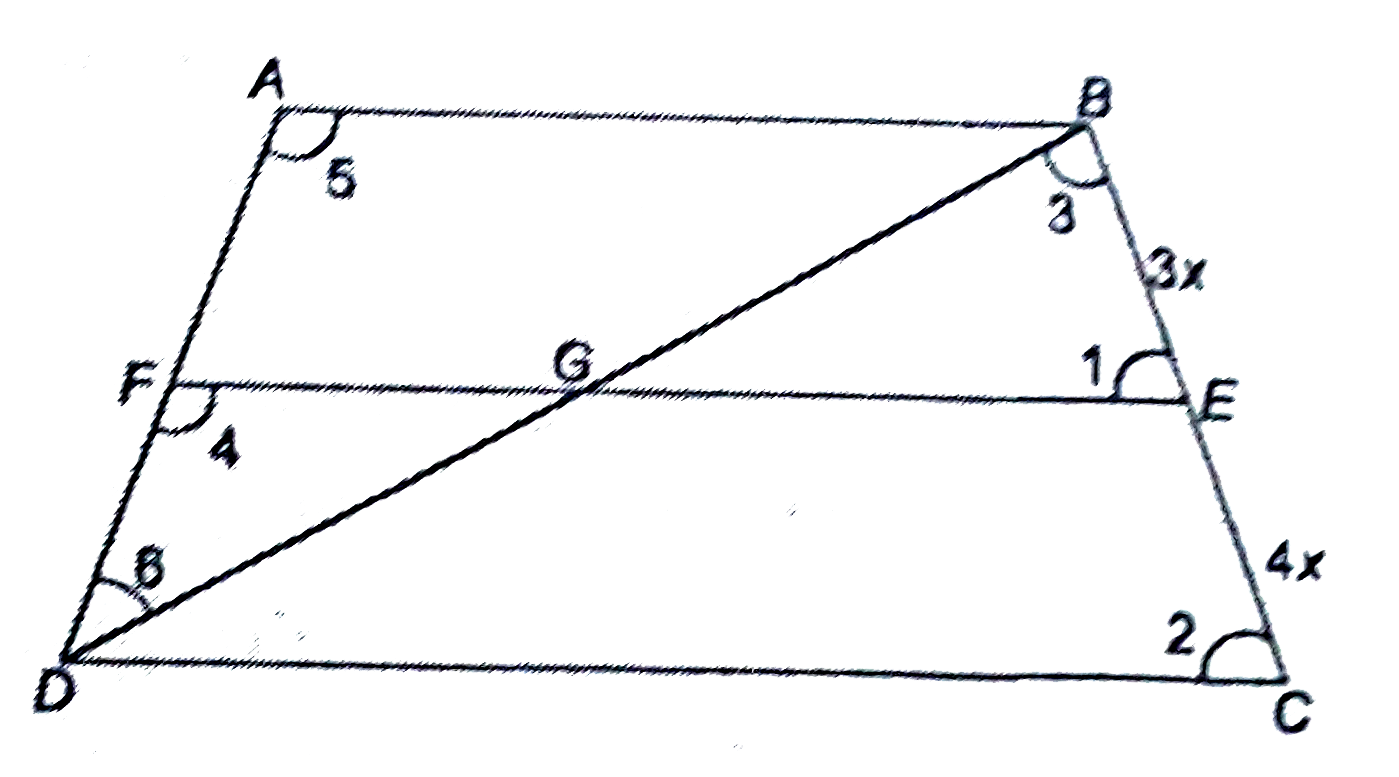
Since GE||DC
(by B.P theorem ) …(1)
Also GF||AB
(by B.P theorem) ….(2)
from (1) and (2) , we get
In
(corresponding as GE||DC)
(common)
(AA corocllary)
(corresponding sides of similar triangles are proportional)
....(4)
Now in
( corresponding as FG||AB)
(common)
(AA corollary)
( from 3)...(5))
Adding (4) and (5) , we get
Hence proved.
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In a trapezium ABCD, AB||DC and DC=2AB. EF drawn parallel to AB cuts AD in F and BC in E such that BEBC=34 .Diagonals DB intersects EF at G. Prove that 7EF=10AB.
View SolutionIn trapezium ABCD, AB||DC and CD = 2AB, EF drawn parallel to AB cuts AO in F and BC in F such that BEEC=34, diagonal DB intersects EF at Q. The find the relation between FE and AB?
View Solution
Knowledge Check
In a trapezium ABCD ,AB||CDandDC=3AB.EF||AB intersects DA and CB at E and F such that BFFC=23 . Then 3DC=
A4EFB2EFC5EfDEFIn a trapezium ABCD, AB||DC, AB = AD, ∠ADC=64∘and∠BCD=54∘. Find ∠DBC.
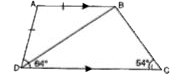 A64∘B72∘C94∘D116∘
A64∘B72∘C94∘D116∘E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
In trapezium ABCD,AB∣∣DCAB=16cm,DC=10cm,AD=CB=5cm then its area is cm2.
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionABCD is a trapezium with AB||DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
View SolutionO is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB||DC. Through O , aline segment PQ is drawn parallel to AB meeting AD in P and BC in Q, prove that PO=QO.
View Solution15 O is the point of intersection of the diagonals AC and BD ofa trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. rove that PO=QO ,
View Solution

