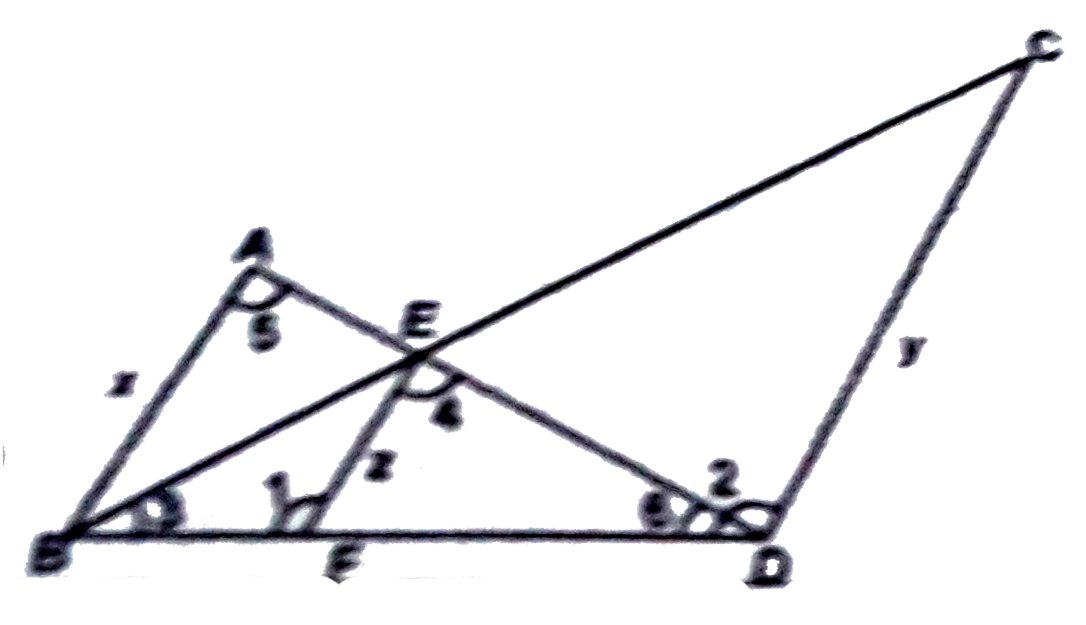
In the adjoining figure , AB||CD||EF.
prove that 1x+1y=1z.
Video Solution
Text Solution
In △BFEand△BDC,
∠1=∠2 ( corresponding ∠s as EF||CD)
∠=∠3 (common)

BFBD=FEDC ( corresponding sides of similar triangles are proportional)
BFBD=zy.....(i)
In △DFEand△DBA
and ∠4=∠5 ( correspending ∠s as EF||AB)
∠6=∠6 (common)

DFDB=FEBA (corresponding sides of similar triangles are proportional)
DFDB=zx...(2)
( Remember , common part in (1) and (2) should be in denominator so that we can add easily) Adding (1) and (2) , we get,
BFBD+DFDB=zy+zx
BF+DFBD=(1y+1x)
BDBD=z(1x+1y)⇒1=z(1x+1y)
1z=1x+1y
|
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
In the adjoining figure AB∣∣CDandPQ=SR, then :
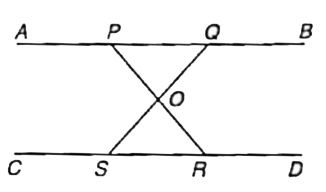 APQ=PSBSR=RPCPS=QRDAP=RD
APQ=PSBSR=RPCPS=QRDAP=RDIn the figure , AB||CD , what is x+y.
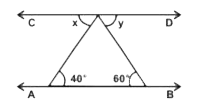 A40∘B60∘C100∘D80∘
A40∘B60∘C100∘D80∘
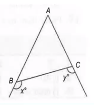
In the adjoining figure, x>y, Prove that AB>AC
View SolutionIn the adjoining figure AB||CD .Find the value of x
View SolutionIn the given figure, AB||CD||EF. Find the value of x.

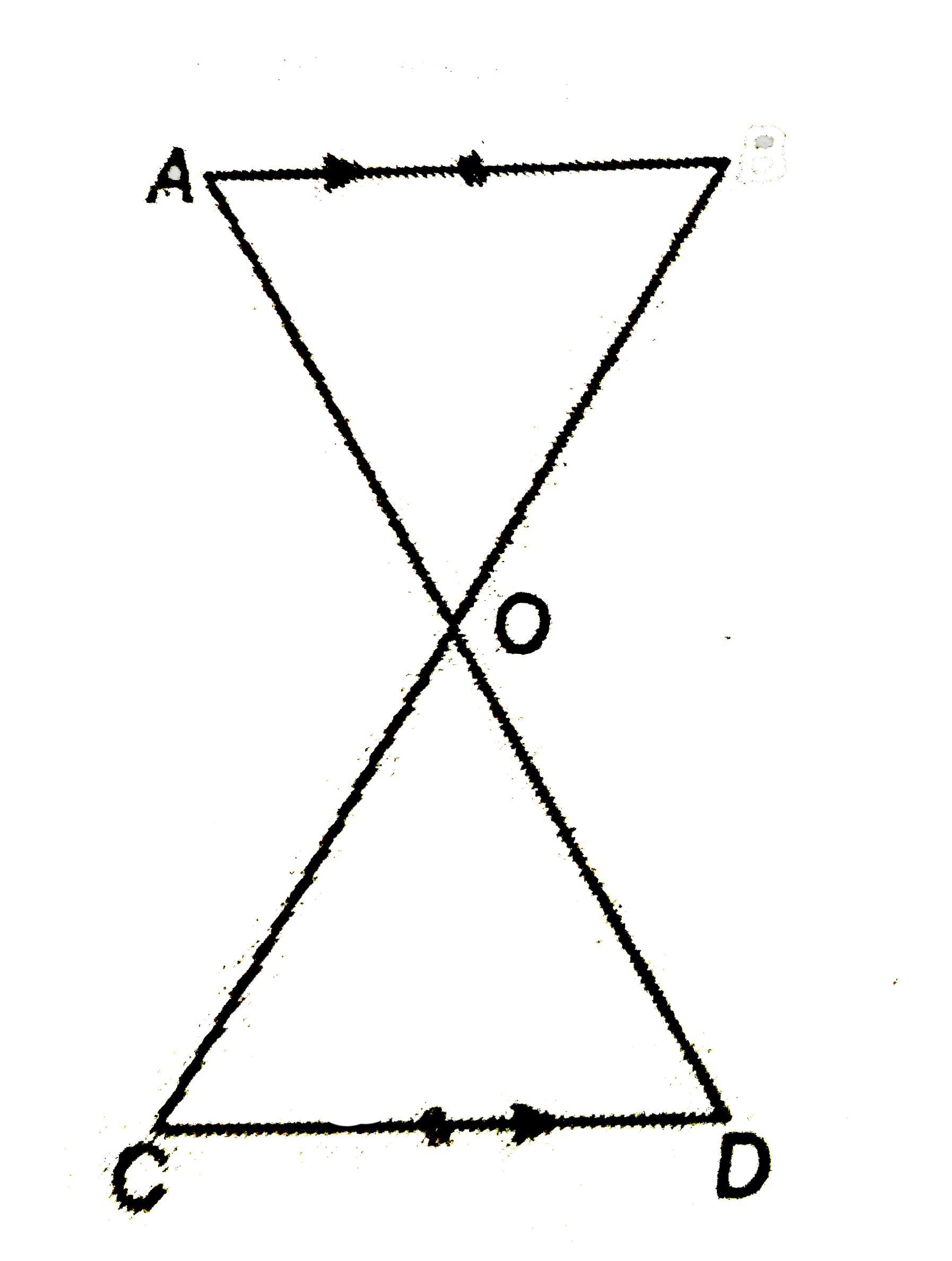
View SolutionIn the adjoining figure AB=CD and AB||CD prove that :
(i) ΔAOB≅ΔDOG
(ii) AD and BC bisect each other at point O.
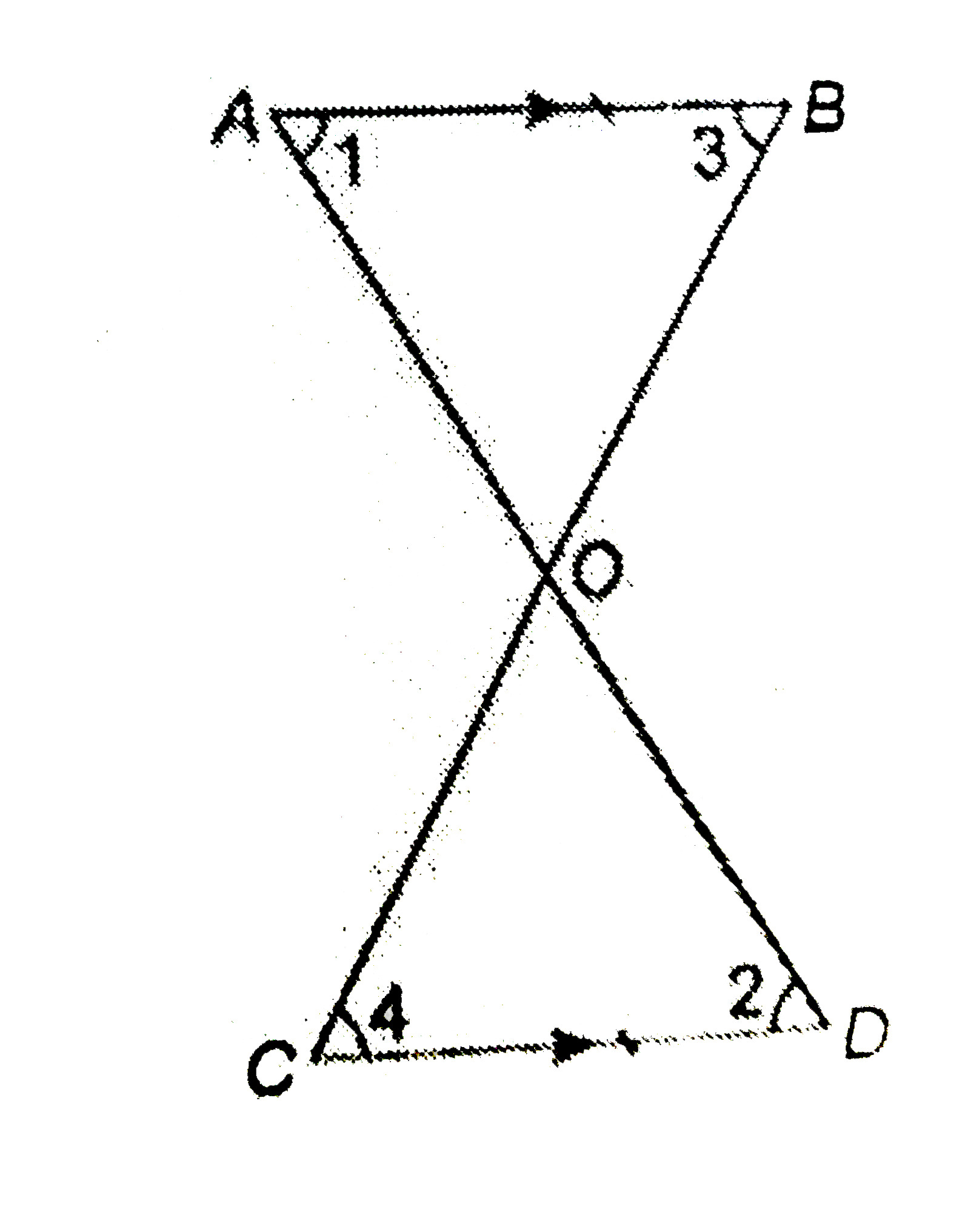
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
View SolutionIn the figure, prove that AB∣∣EF
View Solution

