The motion of a particle, along x-axis, follows the relation x = 8t-3t2 . Here x and t are expressed in metre and second respectively . Find (i) the average velocity of the particle in time interval 0 to 1 s and (ii) its instantaneous velocity at t = 1 s.Solution in Bengali
(i) Let at = 0 , x = x1 and at t =1 , x = x2.
∴ x1=8×0−3×02=0
and x2=8×1=3×12=5m
∴ Displacement =x2−x1=5m and time taken is 1s.
∴ Average velocity =5m1s=5m.s−1.
(ii) Here instantaneous velocity,
v=dxdt=ddt(8t−3t2)=8−2×3t=8−6t
At t = 1 s, dxdt=8−6×1=2m.s−1.
Topper's Solved these Questions
- ONE - DIMENSIONAL MOTION BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - Section Related Questions
17 Videos
- ONE - DIMENSIONAL MOTION BOOK - CHHAYA PUBLICATIONCHAPTER - ONE - DIMENSIONAL MOTION EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
35 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - CBSE SCANNER
19 Videos
- QUESTION PAPERS OF NEET -2017BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF NEET -2017EXERCISE - QUESTION
32 Videos
Similar Questions
Define rest and motion.
View SolutionCan a partical, moving with a uniform speed have a non-uniform velocity?
View SolutionWhat is the reason for absence of atmosphere in some planets?
View SolutionA molecule of a substance has permanent dipole moment p . A mole of this substance is polarised by applying a storg electrostatic field E . The direction of the field is suddenly changed of 60∘ . If N is the avogadro's number the amount of work done by the field is
View SolutionA particle moves along a straight line and its velocity depends on time as v = 3t - t^2. Here, v is in m//s and t in second. Find (a) average velocity and (b) average speed for first five seconds.
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m//s^(2))t-(2m//s^(3))t^(2) . Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View SolutionFigure shows the graph of x-coordinate of a particle moving along x-axis as a function of time. Average velocity during t = 0 to 4 s and instantaneous velocity at t = 4.113 s respectively will be
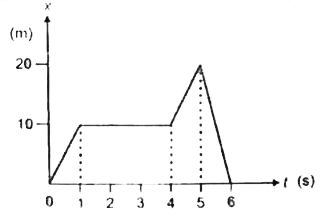
View SolutionFigure shows the graph of x - coordinate of a particle moving along x - axis as a function of time. Average velocity during t = 0 to 6 s and instantaneous velocity at t = 3 s respectively, will be
View SolutionA particle is moving along the x-axis. Its shift from the origin follows the equation: x = 8t-3t ^ 2, where x and t are the units m and s, respectively. (i) Find the average velocity of the particle between t = 0 and t = 1s. What is the instantaneous velocity of the particle at t = 1s?
View Solutionकण के निर्देशांक x = (4t-1) मीटर तथा y=8t2 मीटर है। निम्न की गणना कीजिए -
(i) कण का t=1 सेकण्ड से t=2 सेकण्ड समयान्तराल में औसत वेग तथा
(ii) t= 2 सेकण्ड पर कण का तात्क्षणिक वेग।
View SolutionX-अक्ष के अनुदिश कण का, विस्थापन निम्न प्रकार है -
x=3+8t+7t2
समय t=2 सेकण्ड पर कण का वेग तथा त्वरण ज्ञत करो।
View SolutionA particle moves along a straight line and its velocity depends on time as v = 3t - t^2. Here, v is in m//s and t in second. Find (a) average velocity and (b) average speed for first five seconds.
View SolutionA body moves in a straight line along, x-axis Its distance x (in metre) from the origin Is given by x = 8t- 3t^2 The average speed in the interval t = 0 to t =1 second Is
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View Solution
