A particle is projected with 20ms−1 at 30∘ above horizontal. Find ratio of maximum height to the range of the projectile.
14√3
√34
4√3
4√3
H=u2sin2θ2g
R=v2s2∫hηg
HR−tanθ4
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A particle is projected with velocity u at angle θ1 with horizontal .The ratio of range and maximum height is 4. When it is projected at angle θ2 with horizontal with same speed,the ratio of range and maximum height is 2.Then tanθ1tanθ2 will be equal to
View SolutionA particle is projected at an angle of tan−1(43) with horizontal from a point O.The ratio of the range on the horizontal plane through O to the maximum height ascended above O is
View Solution
Knowledge Check
A particle is projected with 10ms−1 at angle θ above horizontal from a horizontal ground. Find the value of θ so that area under the parabolic path of the projectile will be maximum
(g=10ms−2).A60∘B45∘C90∘DNone of theseA particle is projected with velocity 20ms−1 at angle 60∘ with horizontal . The radius of curvature of trajectory , at the instant when velocity of projectile become perpendicular to velocity of projection is , (g=10ms−1)
A60√3mB80√3mC40√3mD803√3mTwo projectile are projected with the same velocity. If one is projected at an angle of 30∘ to the horizontal. The ratio if maximum heights reached, is:
A1:3B2:1C3:1D:4
A body is projected with a velocity of 30ms−1 at an angle of 30∘ with the vertical. Find the maximum height, time of flight and the horizontal range.
View SolutionTwo particles projected at angles θ1 and θ2(<θ1) to the horizontal attain same maximum height. Which of the two particles has larger range? Find the ratio of their range.
View SolutionA particle is projected with a velocity of 25m/s at an angle of 30∘ with the horizontal . Calculate
(i) The maximum height ,
(ii) time of flight and
(iii) horizontal range .
View SolutionA projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection θ.
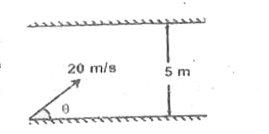
View SolutionA projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
View Solution
