For points and of the coordinates plane, a new distance d (P,Q) is defined by . Let and . Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The area of the ragion bounded by the locus of P and the line in the first quadrant is
2sq.units
4 sq.units
6 sq.units
noen of these
The correct Answer is:B
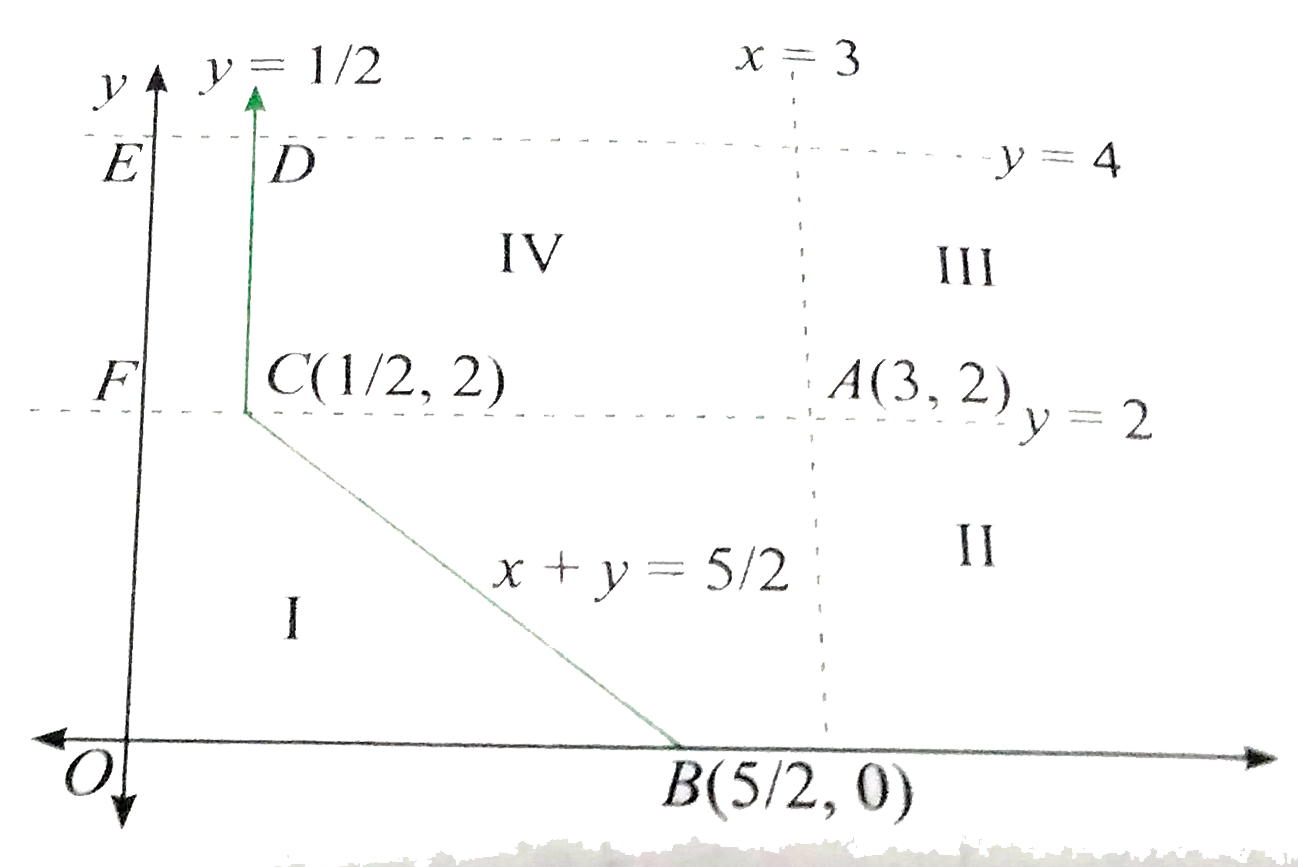
Area of region
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Matrix)
Explore 4 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Numerical)
Explore 12 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Multiple)
Explore 13 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
For points P=(x1,y1)andQ=(x2,y2) of the coordinate plane, a new distance d(P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O(0,0) and A=(3,2). Prove that the set of points in the first quadrant which are equidistant (wrt new distance) from O and A consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram.
View SolutionThe area bounded by the curve y2=9x and the lines x=1,x=4andy=0, in the first quadrant,is
View Solution
Knowledge Check
For points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d(P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The locus of point P isAone -one and onto functionBmany one and onto functionCone-one and into functionDrelation but not functionFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The set of poitns P consists ofAone straight line onlyBunion of two line segmentsCunion of two infinite raysDunion of a line segment of finite length and an infinite rayFor points P≡(x1,y1)andQ=(x2,y2) of the coordinate plane , a new distance d (P,Q) is defined by d(P,Q) =|x1−x2|+|y1−y2| Let O≡(0,0),A≡(1,2)B≡(2,3)andC≡(4,3) are four fixed points on x-y plane
Let R(x,y) such that R is equisdistant from tthe point O and A with respect to new distance and if 0≤x<1and0≤y<2, then R lie on a line segment whose equation isAx+y=3Bx+2y=3C2x+y=3D2x+2y=3
A point P(x,y) moves so that the sum of the distance from P to the coordinate axes is equal to the distance from P to the point A(1,1). The equation of the locus of P in the first quadrant is-
View SolutionThe point P(1,1) is translated parallal to the line 2x=y in the first quadrant through a unit distance.The coordinates of the new position of P are:
View SolutionFor points P≡(x1,y1)andQ=(x2,y2) of the coordinate plane , a new distance d (P,Q) is defined by d(P,Q) =|x1−x2|+|y1−y2| Let O≡(0,0),A≡(1,2)B≡(2,3)andC≡(4,3) are four fixed points on x-y plane
Let S(x,y) such that S is equisdistant from points O and B with respect to new and if x≥2and0≤y<3 then locus of S is
View SolutionFor points P≡(x1,y1)andQ=(x2,y2) of the coordinate plane , a new distance d (P,Q) is defined by d(P,Q) =|x1−x2|+|y1−y2| Let O≡(0,0),A≡(1,2)B≡(2,3)andC≡(4,3) are four fixed points on x-y plane
Le T(x,y) such that T is equisdistant from point O and C with respect to new distance and if T lie in first quadrant , then T consists of the union of a line segment of finite length and an infinite ray whose labelled diagram is
View SolutionThe point P(1,1) is translated parallel to 2x=y in the first quadrant through a unit distance. The coordinates of the new position of P are
View Solution

