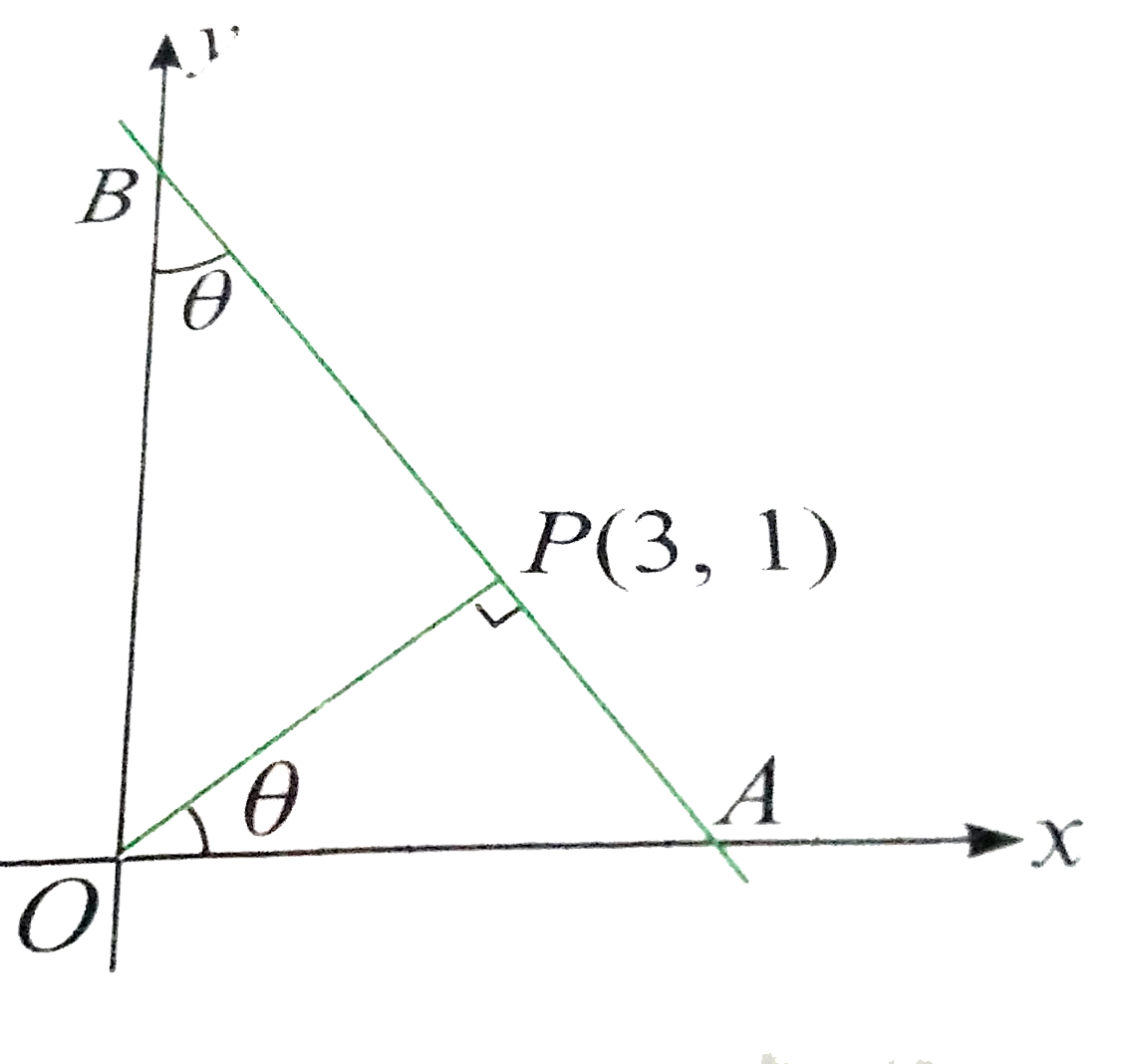
A straight line passing through $P (3, 1)$ meets the coordinate axes at $A$ and $B$ . It is given that the distance of this straight line from the origin $O$ is maximum. The area of triangle $O A B$ is equal to

A

$50 / 3$ sq.units

B

$25 / 3$ sq.units

C

$20 / 3$ sq.units

D

$100 / 3$ sq.units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Line AB will be the farthest from the origin if OP is right angled to the line drawn.
$O P = \sqrt{10}$
Also, $tan θ = \frac{1}{3}$
$O A = O P sec θ$
$= \sqrt{10} \times \frac{\sqrt{10}}{3} = 10$
$O B = O P cos e c θ = \sqrt{10} \times \frac{\sqrt{10}}{1} = 10$
$∴$ Area of $Δ O A B = \frac{1}{2} = \frac{1}{2} (\frac{10}{3} (10) = \frac{50}{3}$

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Equation of straight line passing through origin
AY=mx,
BY=C
CX= my
DX=C

CENGAGE-COORDINATE SYSYEM -Exercise (Single)

Home
Ask Doubt
Profile