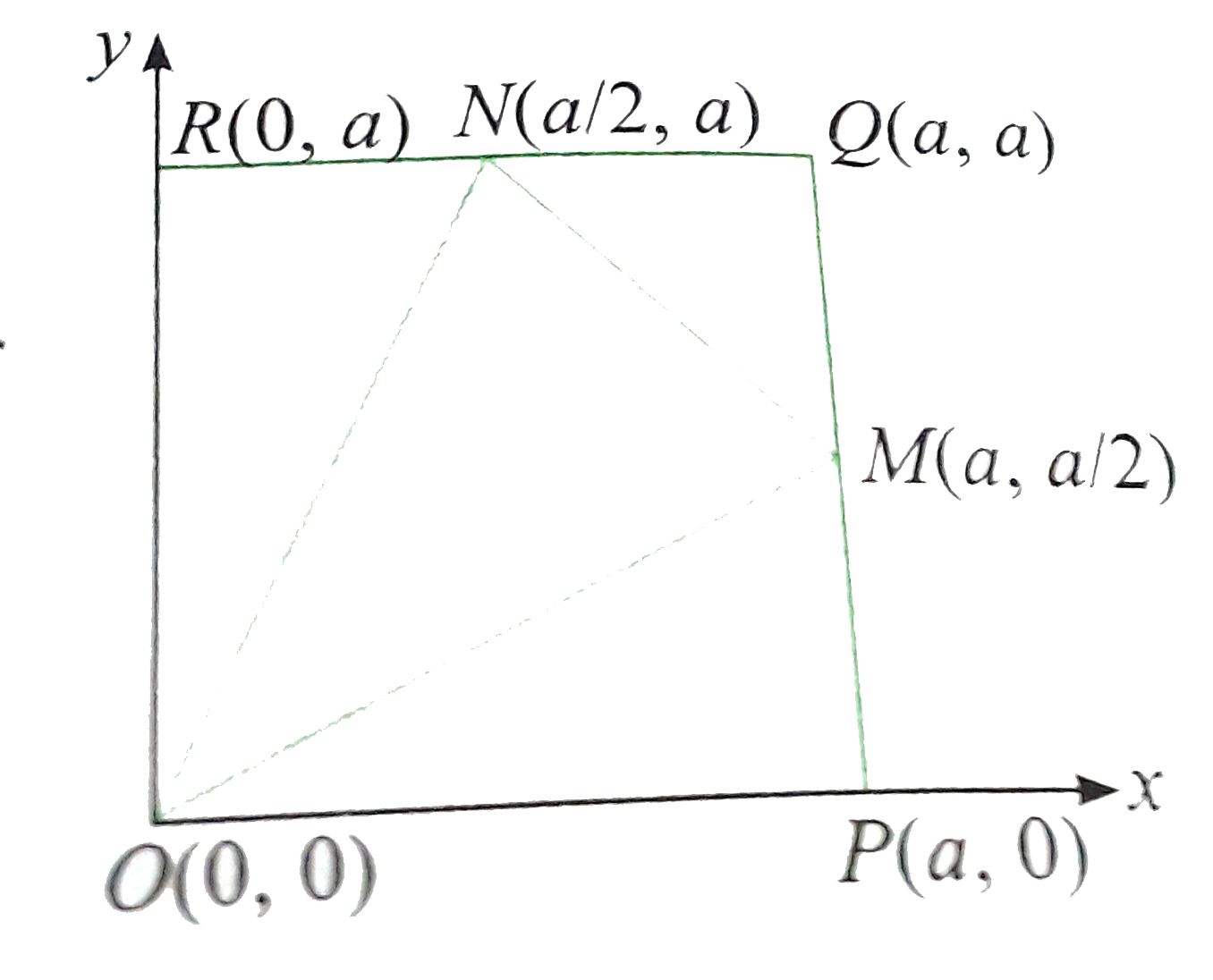
OPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
4:1
2:1
8:3
7:3
The correct Answer is:C
Let the coordinates of vertices O,P,Q,R be (0,0),(a,0)(a,a),(0,a), resepectively. Then we get the coordiantes of M as (a,a/2) and those of N as (a/2,a). Therefore, the area of ΔOMA is
12∣∣
∣
∣∣001aa/21a/2a1∣∣
∣
∣∣=3a28
The area of the sqaure is a2. Hence, the required ratio is 8:3.
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Multiple)
Explore 13 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise (Comprehension)
Explore 10 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.6
Explore 9 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
OPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View Solution
Knowledge Check
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
ABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
View SolutionThe ratio of the area of a square of side a and that of an equilateral triangle of side a, is 2:1 (b) 2:√3 4:3 (d) 4:√3
View SolutionIf a,b∈N, PQRS is a square and P, Q, R, S are mid points of AB, AD, CD, BC respectively then a+b is
View SolutionABCD is a square. E is the mid-point of BC and F is the mid-point of CD . The ratio of the area of triangle AEF to the area of the square ABCD is (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 3 : 8
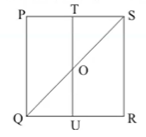
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
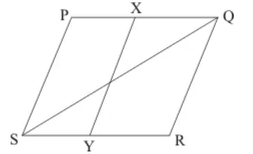
View SolutionIn Figure, PQRS is a parallelogram. If XandY are mid-points of PQandSR respectively and diagonal SQ is jointed. The ratio ar(| |(gm)XQRY):ar(QSR)=
(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1
View Solution

