Convert the following cartesian coordinates x,y=(-1,1)to corresponding poalr coordinates using positive r and negative r.
(i) For the second quadrant point (x,y)≡(−1,1), we have
tanθ=yx=−1⇒θ=3π4
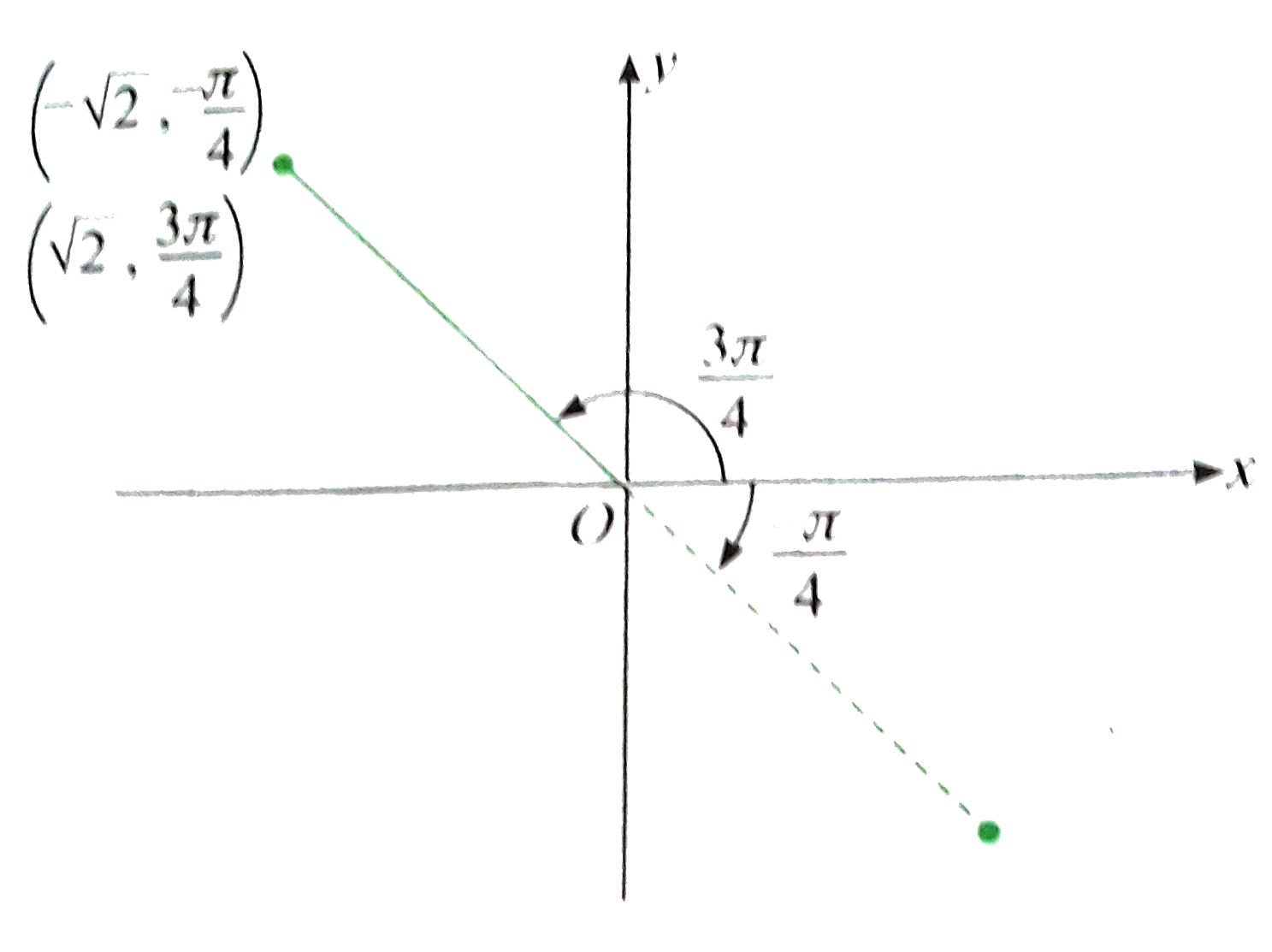
Using positive r, we have
r=√x2+y2=√(−1)2+(1)2=√2
So, one set of polar coordinates is (r,θ)≡(√2,3π/4)
Using negative r, we have coordinates =(−√2,−π/4)
(ii) For the fourth quadrant point (x,y)≡(2,−2), we have
tanθ=−32
⇒θ=tan−1(−32)=−tan−1^32
Using positive r, we have
r=√x2+y2=√(−3)2+(2)2=√13
So, one set of polar coordinates is
(r,θ)≡(√13,−tan−132)
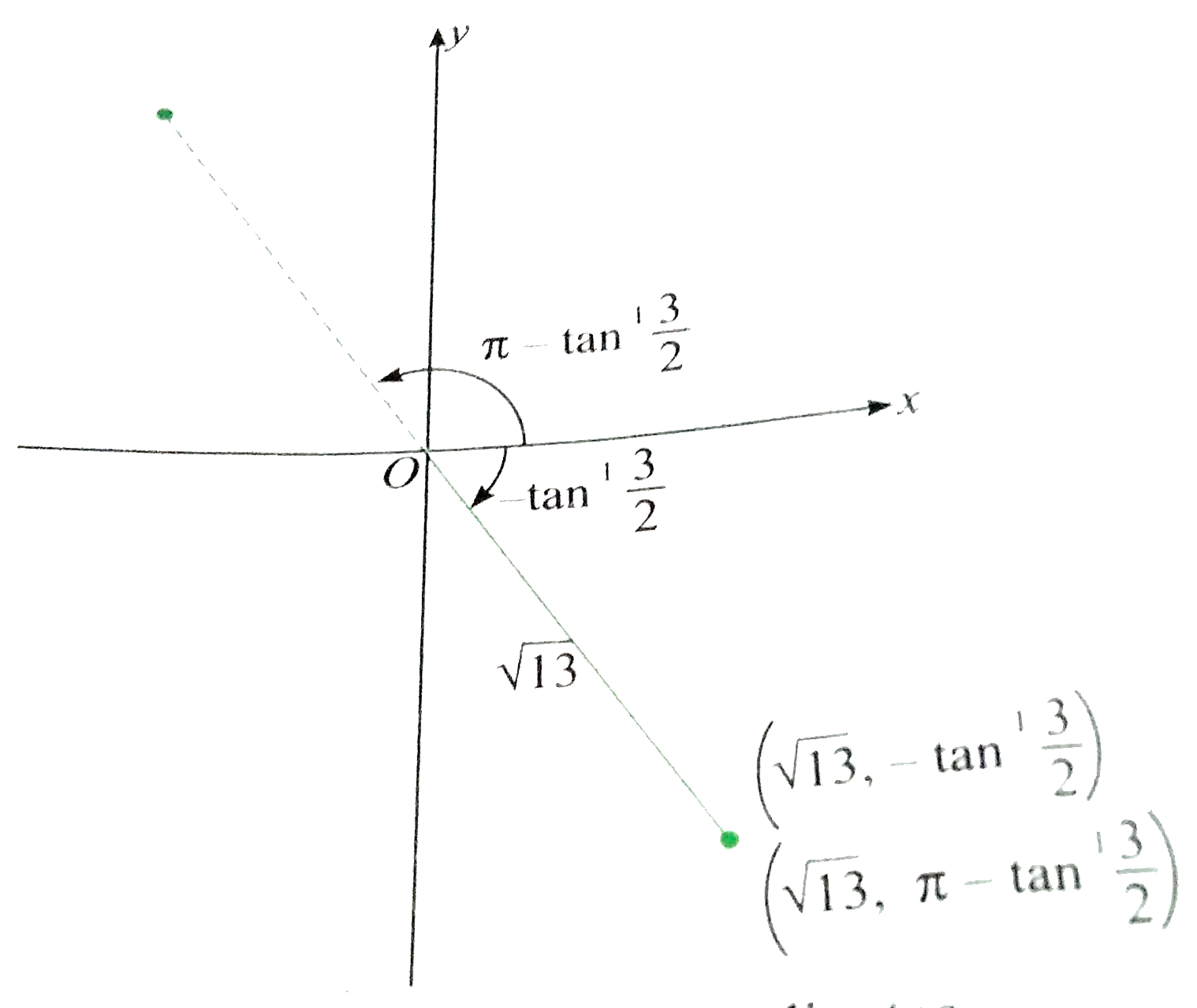
Using negative r, we have coordinates
=(−√13,π−tan−132)
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Conversion of coordinates in Polar conversion form:(i) Convert the following Cartesian coordinates to the corresponding polar coordinates using positive r and negative r . (i)(-1;1) (ii) (2;-3)
View SolutionConvert the following Cartesian coordinates to the cooresponding polar coordinates using positive r.
(i) (1,−1)
(ii) (−3,−4)
View SolutionConvert into Cartesian coordinates:
(2,2π)
View SolutionRepresent the point with cartesian coordinates (1,−1) in terms of polar coordinates.
View SolutionConvert into Cartesian coordinates:
(6√2,π4)
View SolutionConvert the following points from polar coordinates to the corresponding Cartesian coordinates.
(i) (2,π/3)
(ii) (0.π/2)
(iii) (−√2,π/4)
View SolutionConvert Cartesian coordinate into polar coordinate
(2,2)
View SolutionConvert into Cartesian coordinates:
(√2+1√2,π4)
View SolutionConvert polar coordinate into Cartesian coordinate
(2,π4)
View SolutionConvert Cartesian coordinate into polar coordinate
(−1,√3)
View Solution
