The straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
3x+2y=6xy
3x+2y=6
2x+3y=xy
3x+2y=xy
The correct Answer is:D
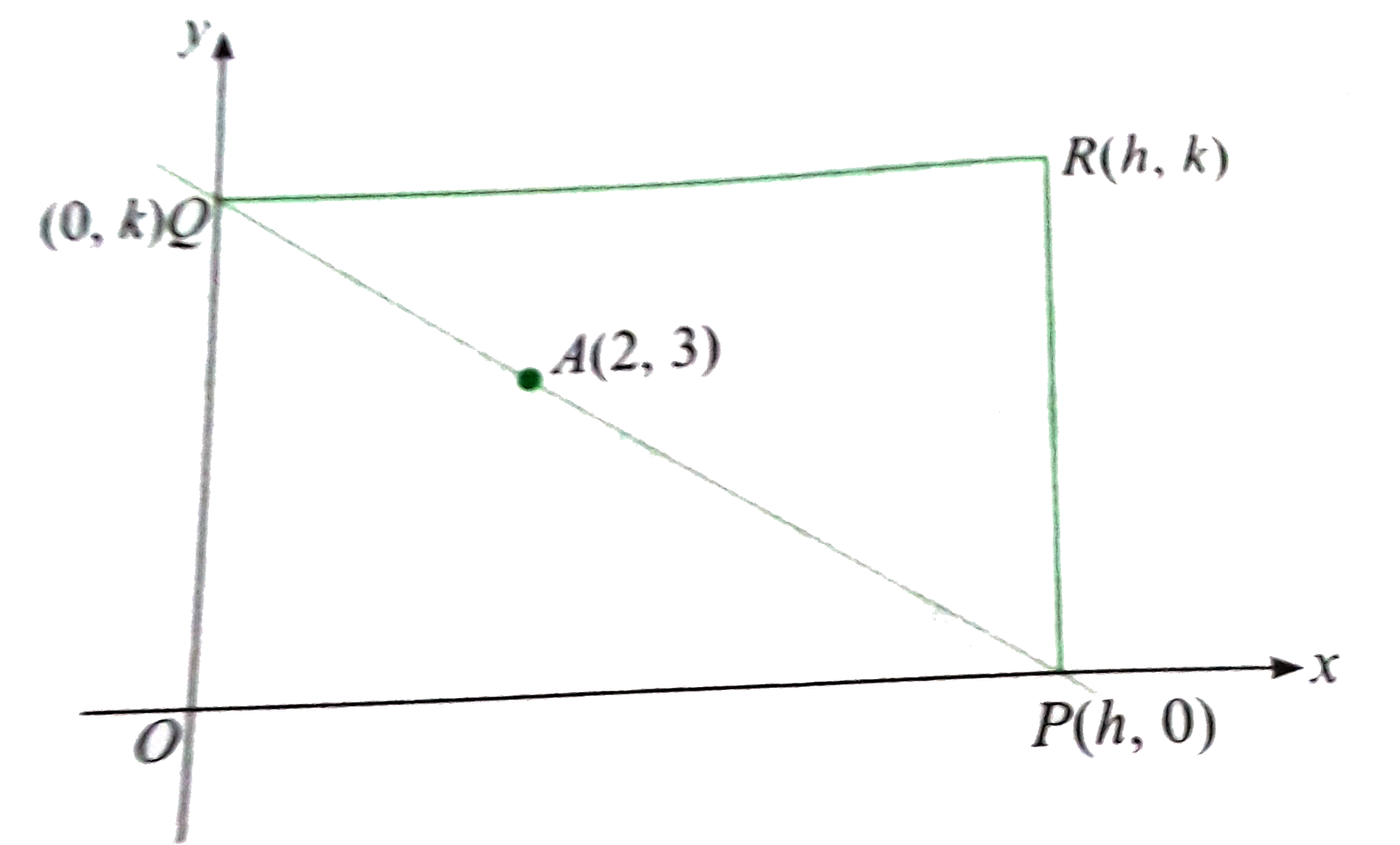
Let the point R be (h,k) .
thus P≡(h,0)andQ≡(0,k)
Equation of variable line PQisxh+yk=1
Point A(2,3) lies on the variable line PQ
∴2h+3k=1
or 2x+3y=1
Therefore, the locus of point R is 2y+3x=xy.
Topper's Solved these Questions
Similar Questions
A variable straight line passes through a fixed point (a,b) intersecting the co-ordinates axes at A & B. If 'O' is the origin, then the locus of the centroid of the triangle OAB is (A) bx+ay−3xy=0 (B) bx+ay−2xy=0 (C) ax+by−3xy=0 (D) ax+by−2xy=0.
View SolutionA straight line passing through the point (87, 33) cuts the positive direction of the coordinate axes at the point P and Q. If Q is the origin then the minimum area of the triangle OPQ is.
View Solution
Knowledge Check
If a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
Ax2+y2−4x2y2=0Bx2+y2−2xy=0Cx2+y2−16x2y2=0Dx2+y2−2x2y2=0If a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct point P and Q. then the locus of the mid- point of PQ is
Ax2+y2−2x2y2=0Bx2+y2−2xy=0Cx2+y2−4x2y2=0Dx2+y2−16x2y2=0A straight line through the point (2,2) intersects the line √3x+y=0 and √3x−y=0 at the points A and B respectively. If O be the origin and ΔOAB be equilateral then the equation of the line AB is
Ax+y−4=0By−2=0Cx−2=0DNone
A straight line passes through a fixed point (2, 3). Locus of the foot of the perpendicular on it drawn from the origin is
View SolutionLine segment AB of fixed length c slides between coordinate axes such that its ends A and B lie on the axes. If O is origin and rectangle OAPB is completed, then show that the locus of the foot of the perpendicular drawn from P to AB is x23+y23=c23.
View SolutionLet (h,k) be a fixed point, where h>0,k>0. A straight line passing through this point cuts the positive direction of the coordinate axes at the point PandQ . Find the minimum area of triangle OPQ,O being the origin.
View SolutionThe variable line drawn through the point (1,3) meets the x-axis at A and y-axis at B. If the rectangle OAPB is completed. Where “O” isthe origin, then locus of “P” is
View SolutionThrough the point (5,12) a straight line is drawn to meet the axes is points A and B. If the rectangle OACB is completed, then locus of the vertex C is
View Solution
