Let k be an integer such that the triangle with vertices (k,−3k),(5,k) and (−k,2) has area 28sq. units. Then the orthocentre of this triangle is at the point : (1,−34) (2) (2,12) (3) (2,−12) (4) (1,34)
(2,12)
(2,−12)
(1,34)
(1,−34)
The correct Answer is:A
We have
12∣∣
∣∣k−3k15k1−k21∣∣
∣∣=±28
⇒5k2+13k−46=0
or 5k2+13k+66=0 (no ral solution)
⇒=K=−235ork=2
Since K is an integer, k=2
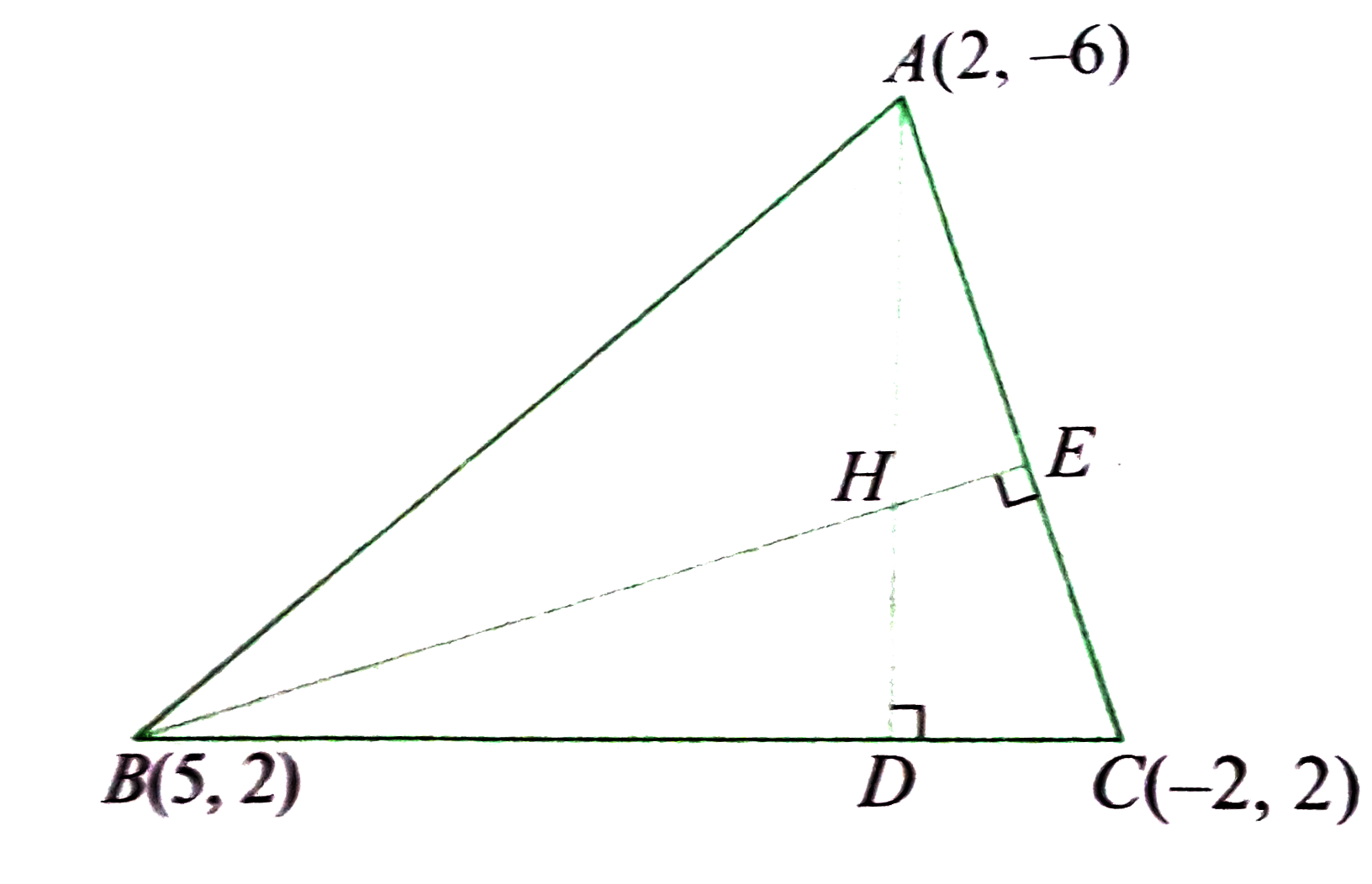
Form the figure, slope of BC is 0. So, equation of AD is
x=2
Slope of AC is 1/2.
Eqaution of line BE is x−2y≡0
Topper's Solved these Questions
Similar Questions
Let k be an integer such that the triangle with vertices (k,−3k),(5,k) and (−k,2) has area 28sq. units. Then the orthocentre of this triangle is at the point : (1,−34) (2) (2,12) (3) (2,−12) (4) (1,34)
View SolutionFind the value of k so that the area of the triangle with vertices (1,−1),(−4,2k)and(−k,−5) is 24 square units.
View Solution
Knowledge Check
Let k be an integer such that the triangle with vertices (k,−3k),(5,k) and (-k, 2) has area 28 sq units. Then, the orthocentre of this triangle is at the point
A(2,12)B(2,−12)C(1,34)D(1,−34)Orthocentre of the triangle formed by joining the points (4,14),(3,13),(2,12) is
A(124,24)B(−124,−24)C(−124,24)D(124,−24)The orthocentre of the triangle with vertices are (-2,-6),(-2,4) and (1,3) is
A(3,1)B(1,1/3)C(1,3)DNone of these
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
View SolutionFind the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k), and (-k, - 5) is 24 sq. units.
View SolutionFind the value of k so that the area of the triangle with vertices A(k+1,1),B(4,−3) and C(7,−k) is 6 square units.
View SolutionThe area of a triangle with vertices (−2,0),(0,k) and (0,4) is 4 square units.Then the values of K will be
View SolutionIf the area of triangle with vertices (2,-6), (5,4) and (k,4) is 35. Then k equal to
View Solution