If vertex A of triangle ABC is (3,5) and centroid is (−1,2), then find the midpoint of side BC.
To solve the problem step-by-step, we need to find the midpoint D of side BC given vertex A of triangle ABC at coordinates (3,5) and the centroid G at coordinates (−1,2).
Step 1: Understand the relationship between the centroid and the vertices of the triangle
The centroid G of a triangle with vertices A(x1,y1), B(x2,y2), and C(x3,y3) is given by the formula:
G=(x1+x2+x33,y1+y2+y33)
In our case, we know A(3,5) and G(−1,2).
Step 2: Set up the equations for the centroid
Let the coordinates of vertices B and C be (x2,y2) and (x3,y3) respectively. From the centroid formula, we can set up the following equations:
−1=3+x2+x33(1)
2=5+y2+y33(2)
Step 3: Solve for x2+x3 and y2+y3
From equation (1):
−1⋅3=3+x2+x3
−3=3+x2+x3⟹x2+x3=−6(3)
From equation (2):
2⋅3=5+y2+y3
6=5+y2+y3⟹y2+y3=1(4)
Step 4: Find the midpoint D of side BC
The midpoint D of side BC can be calculated using the midpoint formula:
D=(x2+x32,y2+y32)
Substituting from equations (3) and (4):
D=(−62,12)
D=(−3,0.5)
Final Answer
The midpoint of side BC is D(−3,0.5).
---
The centroid G of a triangle with vertices A(x1,y1), B(x2,y2), and C(x3,y3) is given by the formula:
G=(x1+x2+x33,y1+y2+y33)
In our case, we know A(3,5) and G(−1,2).
Let the coordinates of vertices B and C be (x2,y2) and (x3,y3) respectively. From the centroid formula, we can set up the following equations:
−1=3+x2+x33(1)
2=5+y2+y33(2)
From equation (1):
−1⋅3=3+x2+x3
−3=3+x2+x3⟹x2+x3=−6(3)
2⋅3=5+y2+y3
6=5+y2+y3⟹y2+y3=1(4)
The midpoint D of side BC can be calculated using the midpoint formula:
D=(x2+x32,y2+y32)
Substituting from equations (3) and (4):
D=(−62,12)
D=(−3,0.5)
The midpoint of side BC is D(−3,0.5).
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
In Δ,A(5,6) and its centroid is (2,3) then midpoint of the side BC is
View SolutionIn ΔABC,A(5,6) and its centroid is (2,3) then mid point of the side BC is
View SolutionA=(1,3,-2) is a vertex of triangle ABC whose centroid is G=(-1,4,2) then length of median through A is
View SolutionIn a triangle ABC ,if the centroid is (2,0) and the mid point of BC is (1,3) then A=
View SolutionIf the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respectively, then find the equation of the side AB.
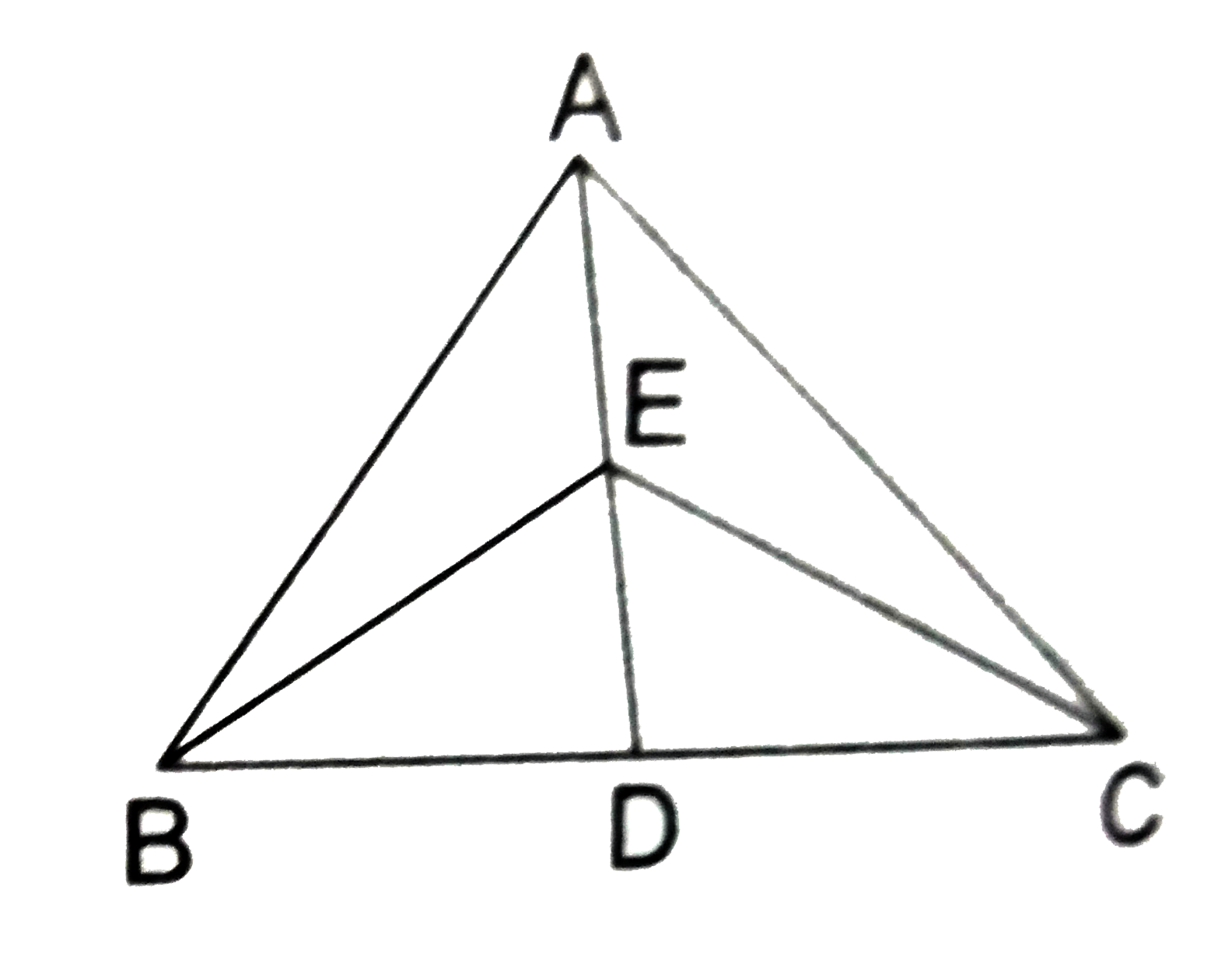
View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
View SolutionTwo vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
View SolutionIf the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respec-tively, then find the equation of the side AB.
View SolutionThe co-ordinates of two vertices of ΔABC are A(3,2,-4) and B(-2,3,-1). If its centroid is (3,1,0), then find the co-ordinates of vertex C.
View SolutionTwo vertices of a triangle are (1,4)and(5,2). If its centroid is (0,−3), find the third vertex.
View Solution
