Given points $P (2, 3), Q (4, - 2), and R (α, 0)$ . Find the value of a if $P R + R Q$ is minimum.

Video Solution

Text Solution

Verified by Experts

(i) Point $R (α, 0)$ lies on x-axis.

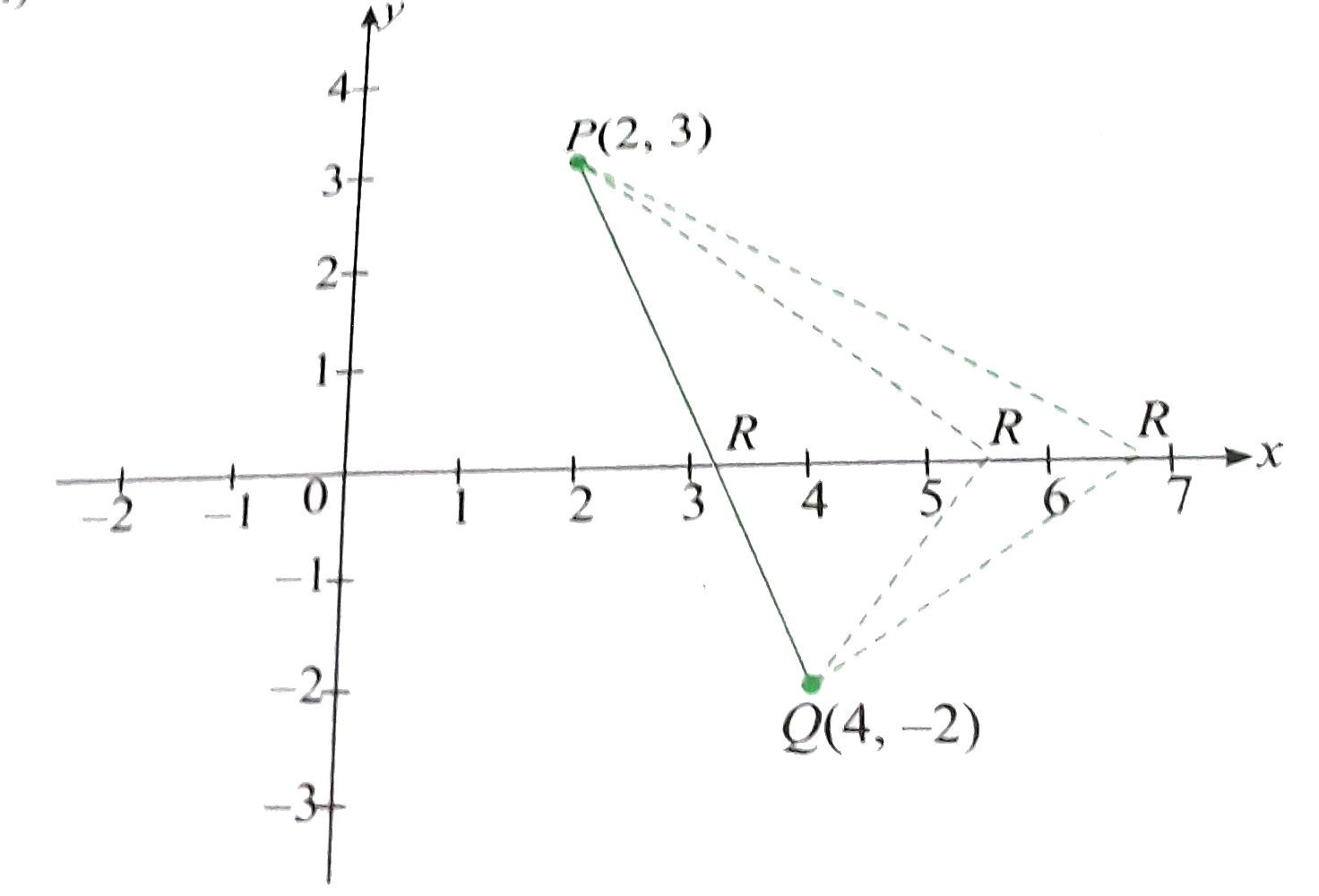
Now, from triangular inequality, $P R + R Q \geq P Q$
Thus minimum value of $P R + R Q$ is PQ, which occurs when points $P, Q$ and R are collinear.
$\Rightarrow ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} 2 & 3 4 & - 2 α & 0 2 & 3 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣ = 0$
$\Rightarrow - 4 - 12 + 2 α + 3 α = 0$
$\Rightarrow α = 16 / 5$
(ii)
Image of Q in x-axis is $Q' (4, 2)$ .
Now, $R Q = R Q$ '
$∴ | P R - R Q | = | P R - R Q' |$
From triangle inequality,
$| P R - P Q' | \leq P Q$ '.
$∴ {| P R - P Q' |}_{max} = P Q'$ , when $P, Q$ ' and R are collinear
$∴ ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} 2 & 3 4 & 2 α & 0 2 & 3 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣ = 0$
$\Rightarrow 4 - 12 - 2 α + 3 α = 0$
$\Rightarrow α = 8$

Updated on:21/07/2023

The mid-point of (3p,4) and (-2, 2q) is (2,6). Find the value of p + q:
A5
B6
C7
D8
If P,Q and R are three points with the co-ordinates (1,4),(4,2) and (m, 2m -1) respectively then the value of m for which PR + RQ is minimum will be equal to
A $\frac{17}{8}$
B $\frac{5}{2}$
C $\frac{7}{2}$
D $\frac{15}{8}$
If $P = (1, 1), Q = (3, 2)$ and $R$ is a point on x-axis then the value of $P R + R Q$ will be minimum at
A $(\frac{5}{3}, 0)$
B $(\frac{1}{3}, 0)$
C $(3, 0)$
D $(1, 0)$