Given that P(3,1),Q(6.5), and R(x,y) are three points such that the angle PRQ is a right angle and the area of RQP is 7, find the number of such points R.
Clearly, R lies on the circle with P and Q as end points of diameter.
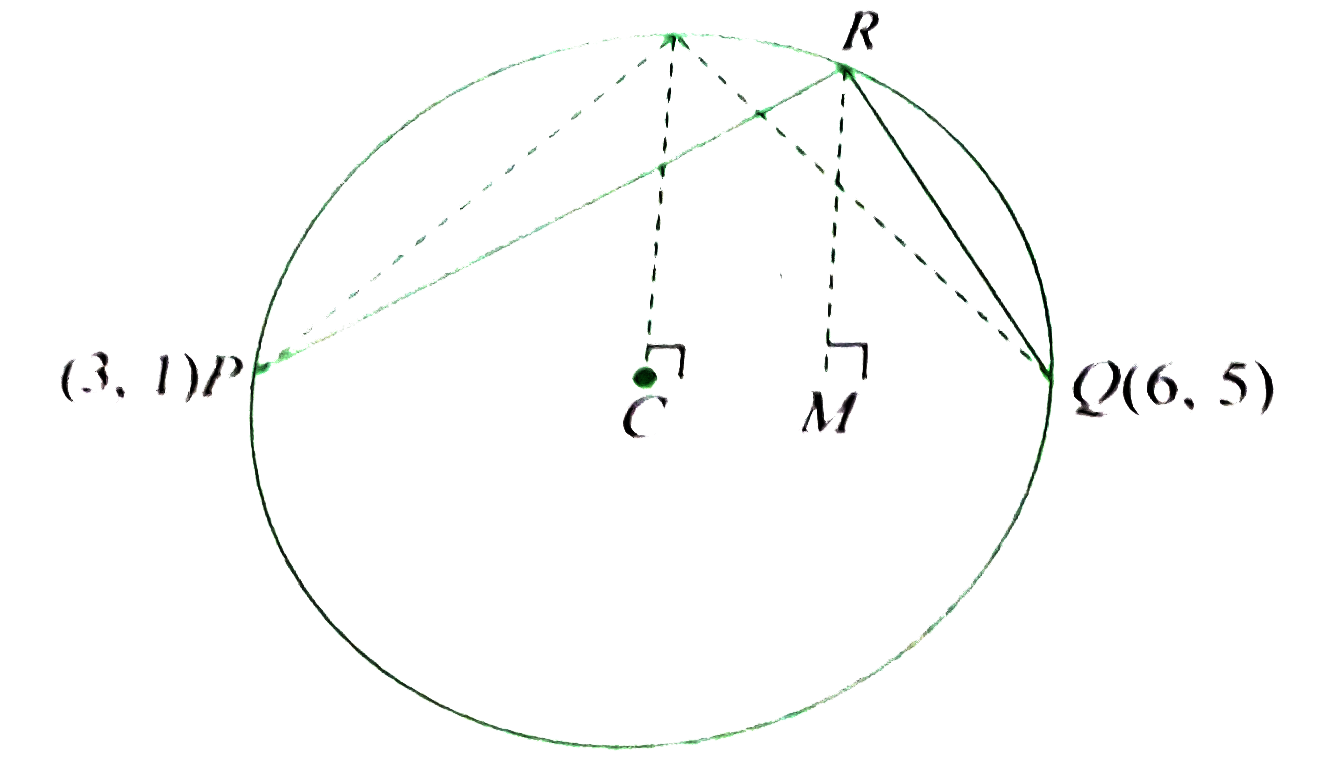
Now, PQ=√(6−3)2+(5−1)2=5
therfore Radius, r=2.5
Now, area of triangle PQR=(12)RM.PQ=7
⇒Rm=145=2.8,
which is not possible as RM cannot be more than radius Hence, no such triangle is possible.
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.1
Explore 6 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.2
Explore 8 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
Given that P(3,1),Q(6.5), and R(x,y) are three points such that the angle PQR is a right angle and the area of RQP is 7, find the number of such points R.
View SolutionIf the line segment joining P(2, 3) and Q(5, 7) subtends a right angle at R(x, y) and the area of ΔPQR=2 sq. units, then the maximum number of such points R is xy - plane are
View Solution
Knowledge Check
P(3, 1), Q(6, 5) and R(x, y) are three points such that the angle PRQ is a right angle and the area of ΔPRQ is 7. The number of such points R that are possible is
A0B1C2D3P(3, 1), Q(6, 5) and R(x, y) are three points such that the angle RPQ is a right angle and the area of ΔRPQ is 7. The number of such points R that are possible is
AA) 1BB) 2CC) 3DD) 4ΔPQR is right angled at Q. If ∠R=30∘, then find the value of (cos P -1/3).
A1/6B(2√2−1)√2C−1/√3D(√3−4)/2√3
Consider the points P(2,−4):Q(4,−2)andR(7,1). The points P,Q,R
View SolutionVerify that point P (-2,2), Q (2,2) and R (2,7) are vertices of a right angled triangle .
View SolutionShow that the points P(-1, -1), Q(2,3) and R(2,6) are the vertices of a right-angled triangle.
View SolutionIf P(p), Q(q), R(r) and S(s) be four points such that 3p+8q=6r+5s then the lines PQ and RS are
View SolutionGiven that P 12, Q = 5 and R = 13 also P+Q=R, then the angle between P and Q will be
View Solution