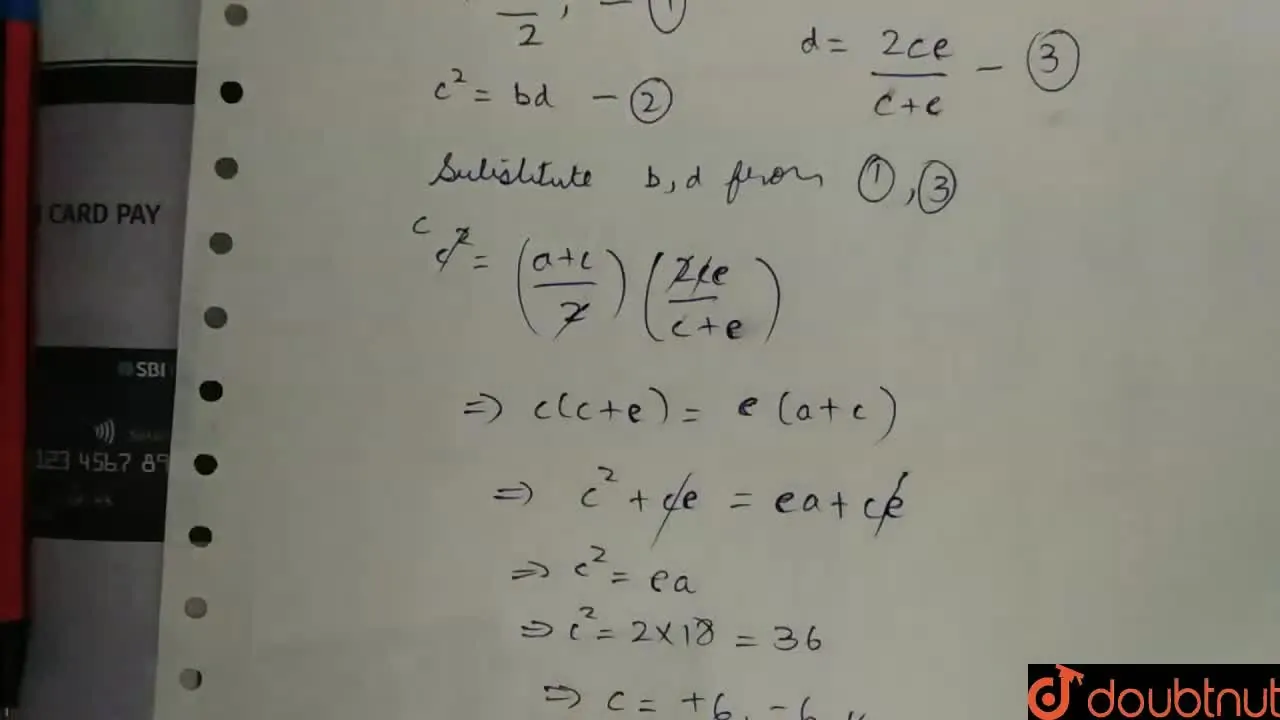Given a,b,c are in A.P. b,c,d are in G.P. and c,d,e are in H.P. if a=2ande=18, then the possible value of 'c' can be :
9
−6
6
−9
The correct Answer is:B, C
Step by step video, text & image solution for Given a,b,c are in A.P. b,c,d are in G.P. and c,d,e are in H.P. if a =2 and e =18, then the possible value of 'c' can be : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VK JAISWALCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)17videos
SEQUENCE AND SERIES
- BOOK - VK JAISWALCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (MATCHING TYPE PROBLEMS)6videos
SEQUENCE AND SERIES
- BOOK - VK JAISWALCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)21videos
SEQUENCE AND SERIES
- BOOK - VK JAISWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)45videos
QUADRATIC EQUATIONS
- BOOK - VK JAISWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems13videos
SOLUTION OF TRIANGLES
Similar Questions
Given a,b,c are in A.P. b,c,d are in G.P. and c,d,e are in H.P. If a=2ad≠=18, then the sum of all possible value of c is ________.
View SolutionGiven a,b,c are in A.P.,b,c,d are in G.P and c,d,e are in H.P .If a=2 and e=18 , then the sum of all possible value of c is ________.
View Solutionif a,b,c are in A.P. b,c,d are in G.P. and c,d,e are in H.P then a,c,e are in
View SolutionIf a,b,c, are in A.P., b,c,d are in G.P. and c,d,e, are in H.P., then a,c,e are in
View SolutionLet a,b,c,d and e be five real numbers such that a,b,c are in AP, b,c,d are GP, c,d,e are in H.P. If a=2 and e=18 then find all possible values of b,c and d.
View SolutionIf a,b,c are is AP; b,c,d are is GP and c,d, c are is H.P then a,c,c are is
View SolutionIf a,b,c are in H.P, b,c,d are in G.P and c,d,e are in A.P. , then the value of e is
View SolutionIf a,b,c, are in A.P., b,c,d are in G.P. and c,d,e, are in H.P., then a,c,e are in
View SolutionIf a,b,c are in A.P. b, c,d are in G.P. and c,d,e are in H.P., then which one of the following is true :
View SolutionIf a,b,c are in A.P. b, c,d are in G.P. and c,d,e are in H.P., then which one of the following is true :
View Solution