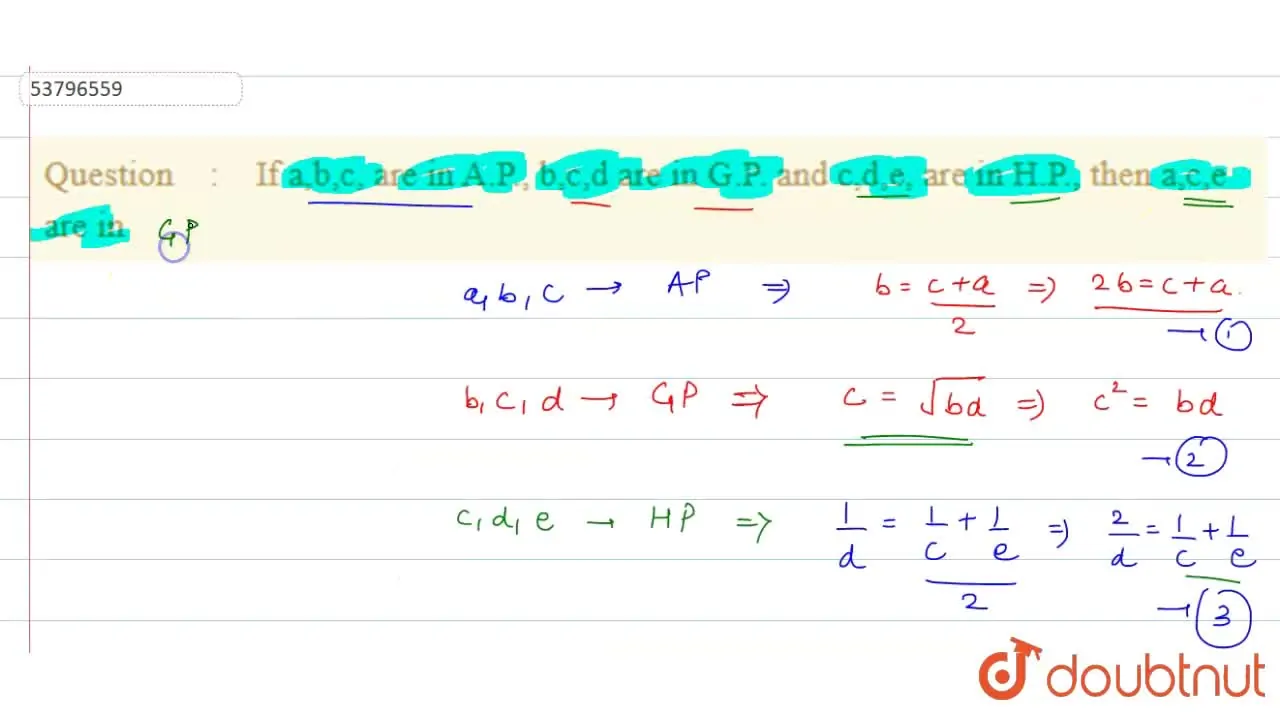
If a,b,c, are in A.P., b,c,d are in G.P. and c,d,e, are in H.P., then a,c,e are in
A.P.
G.P.
H.P.
none of these
The correct Answer is:B
Step by step video, text & image solution for If a,b,c, are in A.P., b,c,d are in G.P. and c,d,e, are in H.P., then a,c,e are in by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test60videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Section II - Assertion Reason Type13videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test50videos
QUADRATIC EXPRESSIONS AND EQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test30videos
SETS
Similar Questions
Let a,b,c,d, e ar non-zero and distinct positive real numbers. If a,b, c are In a,b,c are in A.B, b,c, dare in G.P. and c,d e are in H.P, the a,c,e are in :
View SolutionIf a,b,c are in A.P. b, c,d are in G.P. and c,d,e are in H.P., then which one of the following is true :
View SolutionIf a,b,c, are in A.P., b,c,d are in G.P. and c,d,e, are in H.P., then a,c,e are in
View SolutionIf a,b,c are in H.P, b,c,d are in G.P and c,d,e are in A.P. , then the value of e is
View SolutionIf a,b,c,d,e be 5 numbers such that a,b,c are in A.P; b,c,d are in GP & c,d,e are in HP then prove that a,c,e are in GP
View SolutionIf a,b,c are is AP; b,c,d are is GP and c,d, c are is H.P then a,c,c are is
View SolutionIf a,b,c are in A.P. b, c,d are in G.P. and c,d,e are in H.P., then which one of the following is true :
View SolutionGiven a,b,c are in A.P. b,c,d are in G.P. and c,d,e are in H.P. if a=2ande=18, then the possible value of 'c' can be :
View SolutionGiven a,b,c are in A.P.,b,c,d are in G.P and c,d,e are in H.P .If a=2 and e=18 , then the sum of all possible value of c is ________.
View SolutionGiven a,b,c are in A.P. b,c,d are in G.P. and c,d,e are in H.P. If a=2ad≠=18, then the sum of all possible value of c is ________.
View Solution