Question

Find the number of solution of
$2x^2+3^x+4^x-5^x=0$

Explanation

We have `2^(x)+3^(x)+ 4^(x)-5^(x)=0`
`rArr" "2^(x)+3^(x)+4^(x)= 5^(x)`
`rArr" "((2)/(5))^(x)+ ((3)/(5))^(x)+ ((4)/(5))^(x)=1`
Now the number of solutions ti the equation is equal to the number of times the graphs of `y= f(x)= ((2)/(5))^(x)+ ((3)/(5))^(x)+ ((4)/(5))^(x) and y=1` intersect.
For `f(x)= ((2)/(5))^(x)+ ((3)/(5))^(x)+ ((4)/(5))^(x), f(0)=3`
Since the base of each term is less then one, the value of each term and hence the value of `f(x)` decrease when the value of x increases.
When `x to -oo, f(x) to oo` and when `x to oo, f(x) to 0`.
Thus, the graphs of `y= f(x) and y=1` are as shown in the following figure.

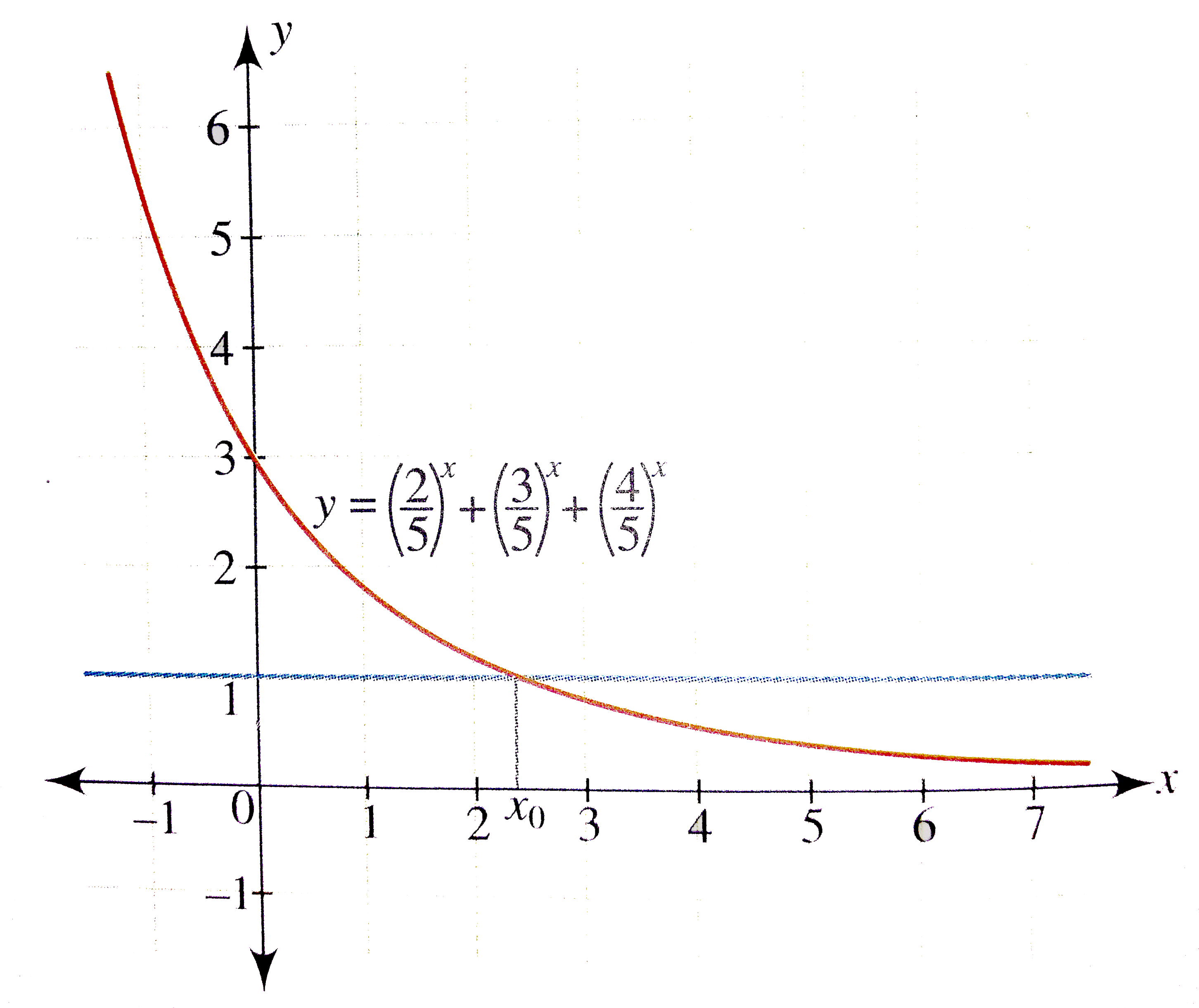
From the graph, there is only one solution `x= x_(o)`.