Find the value of $a$ for which $a x^{2} + (a - 3) x + 1 < 0$ for at least one positive real $x$ .

Video Solution

Text Solution

Verified by Experts

Let $f (x) = a x^{2} + (a - 3) x + 1$
Case (i)
If $a > 0$ , then $f (x)$ will be negative only for those values of x which lie between the roots.
Since $f (0) = 1 > 0$ , the favourable graph according to the questions is shown in the following figure.

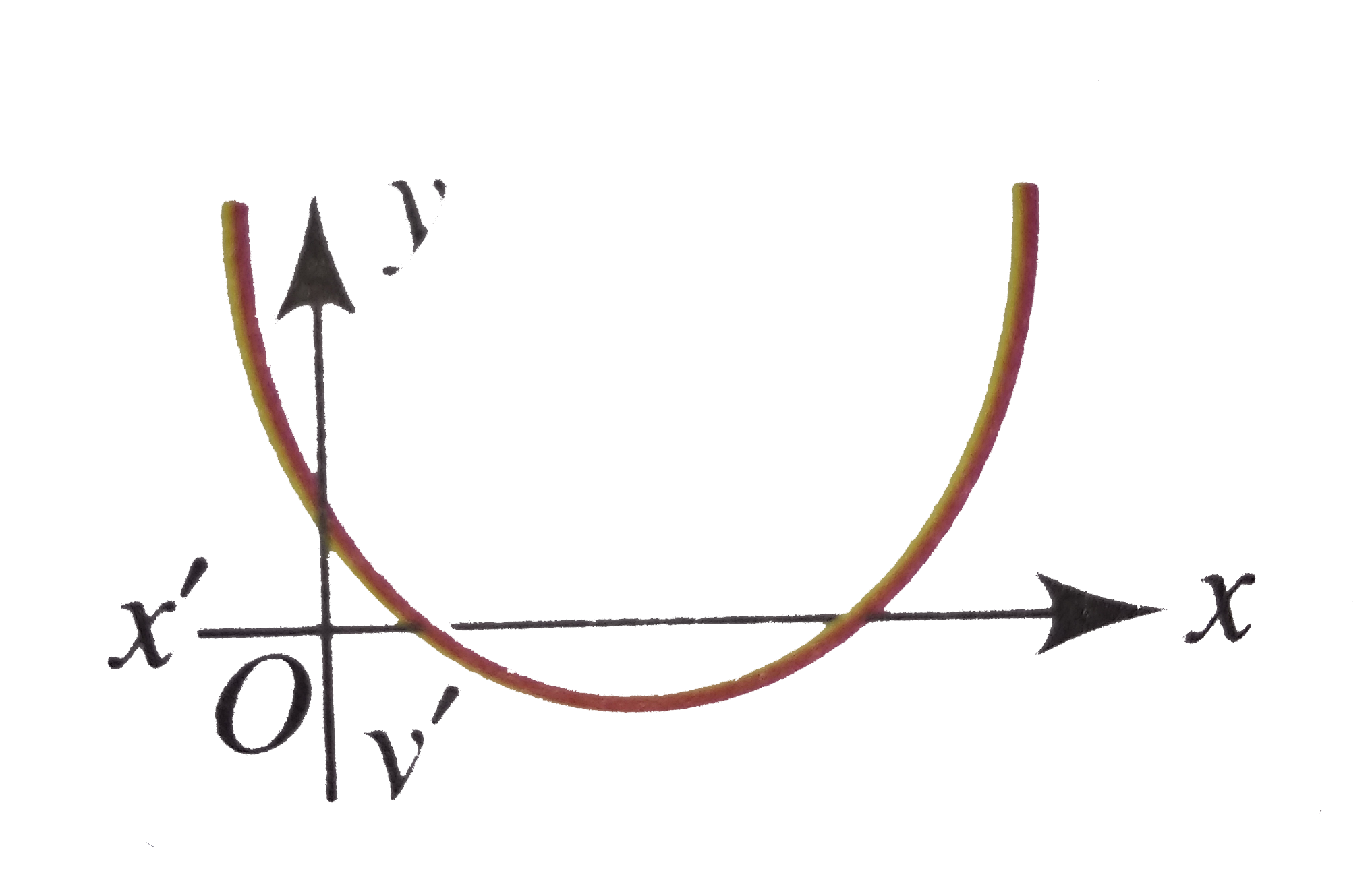
From the graph, we can see that both the roots are positive.
For this
(i) $D > 0 \Rightarrow {(a - 3)}^{2} - 4 a > 0$
$\Rightarrow a < 1 or a > 9$ (i)
(ii) Sum $> 0$ and product $> 0$
$\Rightarrow - (a - 3) > 0 and 1 / a > 0$
$\Rightarrow a < 3$ (ii)
From (i) and (ii), $a < 1$
But $a > 0 \Rightarrow a \in (0, 1)$
Case (ii) : $a < 0$
Since $f (0) = 1 > 0$ , the graph is as shown in the following figure :

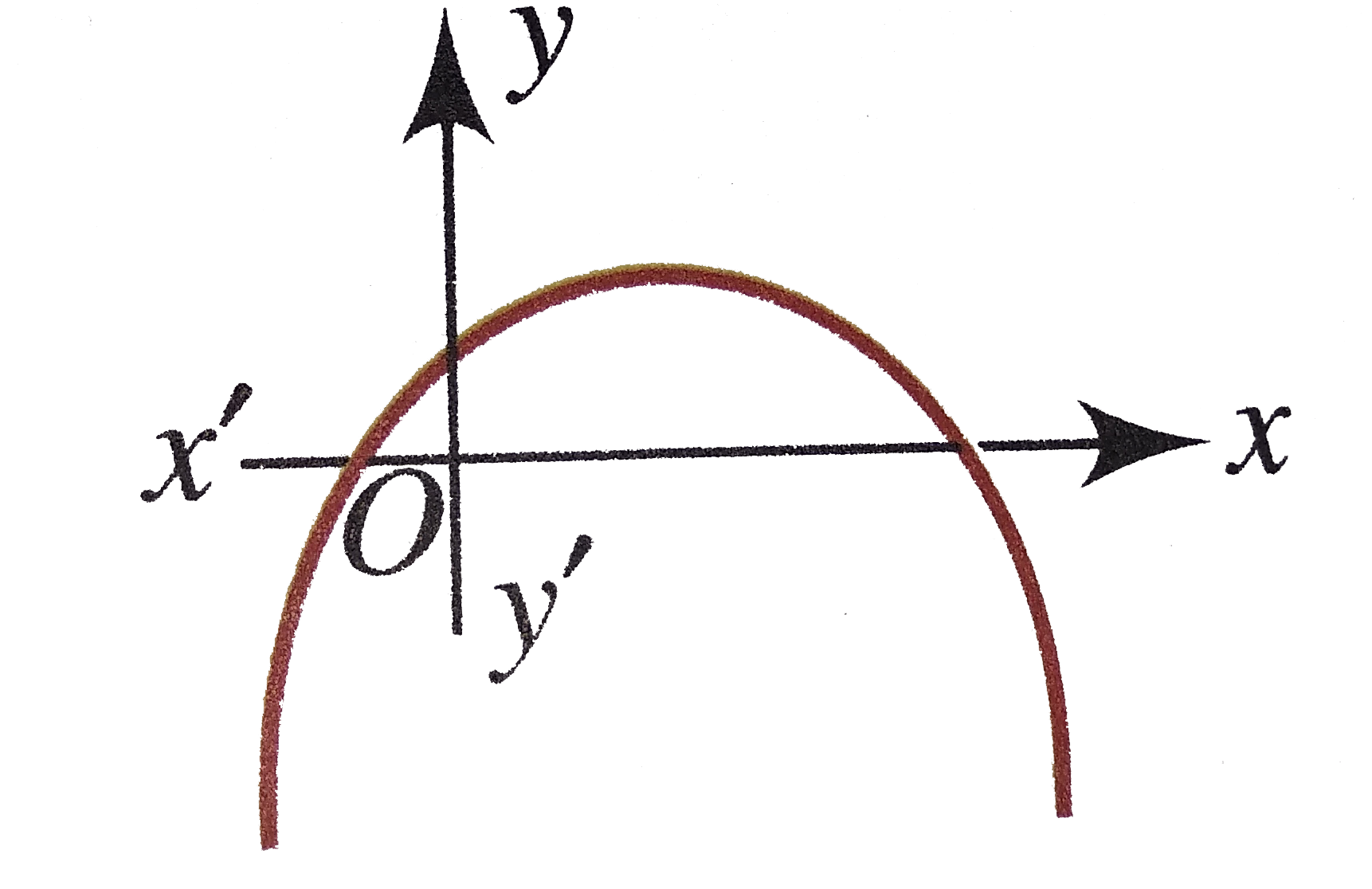
From the graph $a x^{2} + a (a - 3) x + 1 < 0$ , for at least one positive x.
Case (iii): $a = 0$
If $a = 0, f (x) = - 3 x + 1$
$\Rightarrow f (x) < 0, \forall x > 1 / 3$
Thus, from all the cases, the required set of values of $' a'$ is $(- \infty, 1)$ .

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile