Draw the graph of f(x)=4x3−3x and hence draw the graph of g(x)=cos−1(4x3−3x).
Video Solution
Text Solution
f(x)=4x3−3x
∴f'(x)=12x2−3
f'(x)=0∴x=±1/2
Also f(x) is an odd function.
x=1/2 is the point of minima and x=−1/2 is the point of maxima.
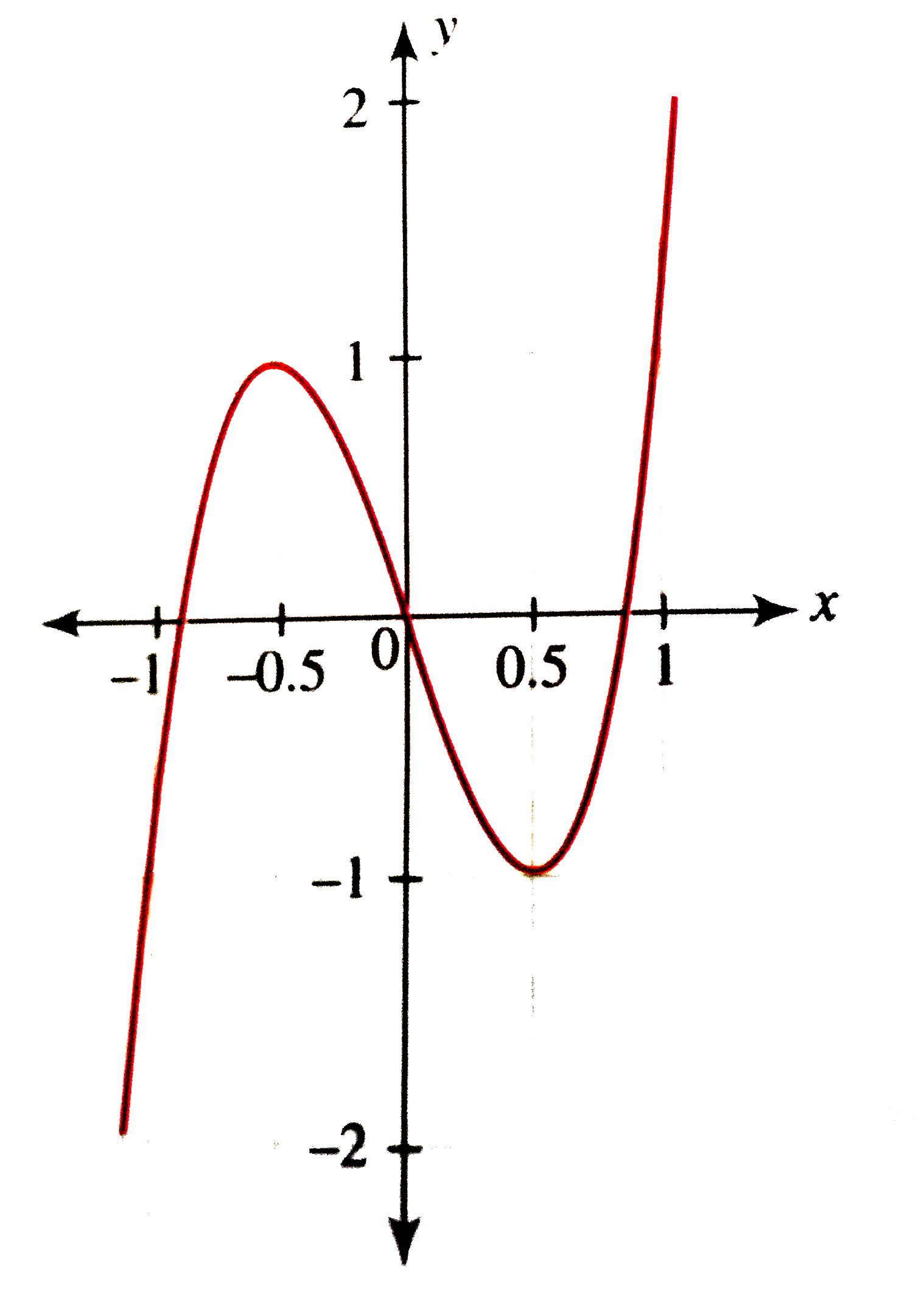
Now for g(x)=cos−1(4x3−3x)=cos−1f(x),
4x3−3x∈[−1,1] for which x∈[−1,1]
So we consider the following graph of y=f(x) for x∈[−1,1].
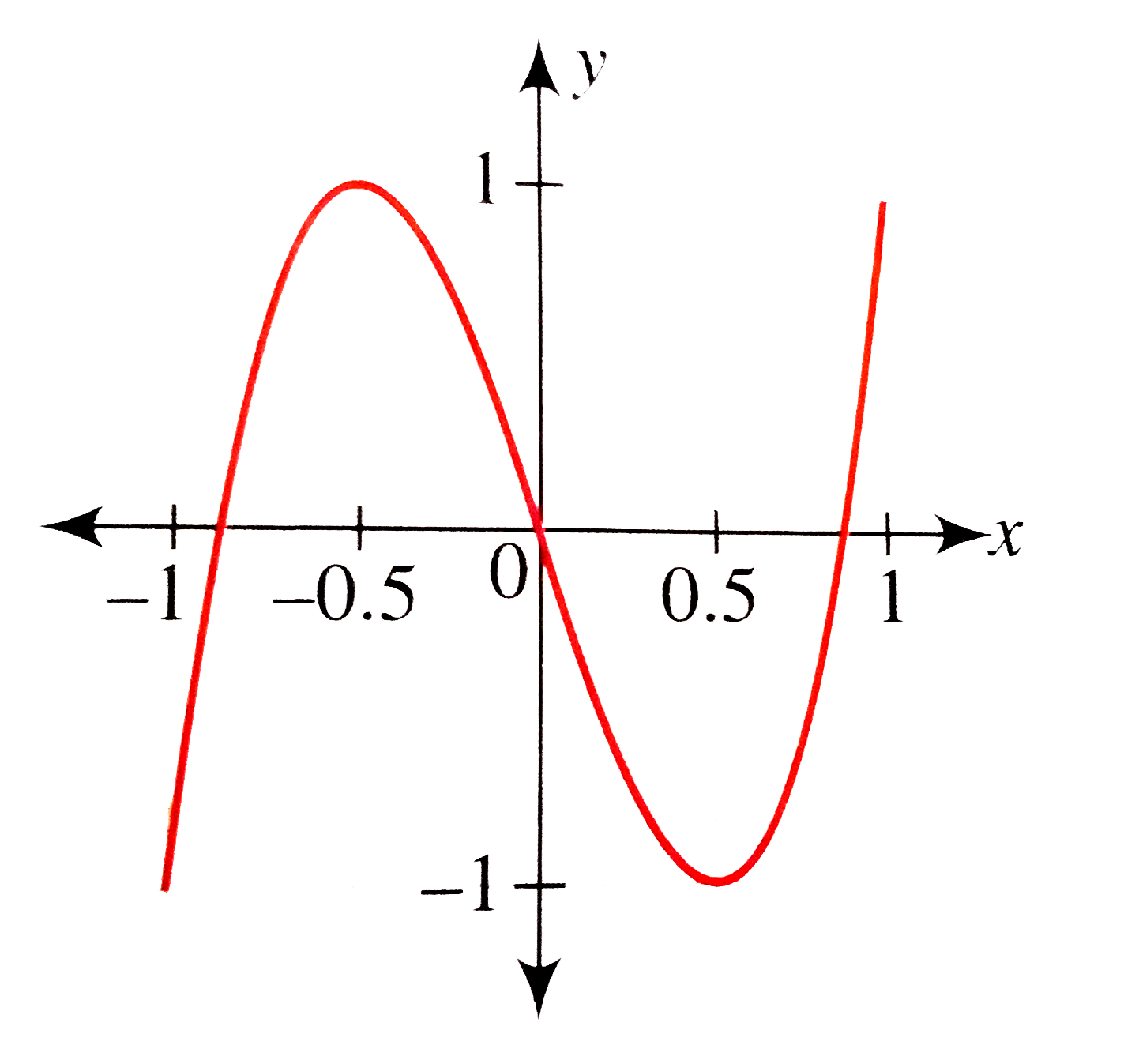
Now g(−1)=cos−1f(−1)=cos−1(−1)=π
g(−1/2)=cos−1f(−1/2)=cos−1(1)=0
g(0)=cos−1f(0)=cos−1(0)=π/2
g(1/2)=cos−1f(1/2)=cos−1(−1)=π
g(1)=cos−1f(1)=cos−1(1)=0
Also g'(x)=f'(x)√1−(f(x))2
So g(x) in non-differentiable at x=±1/2.
Hence the graph of g(x)=cos−1(4x3−3x) is as shown in the following figure.
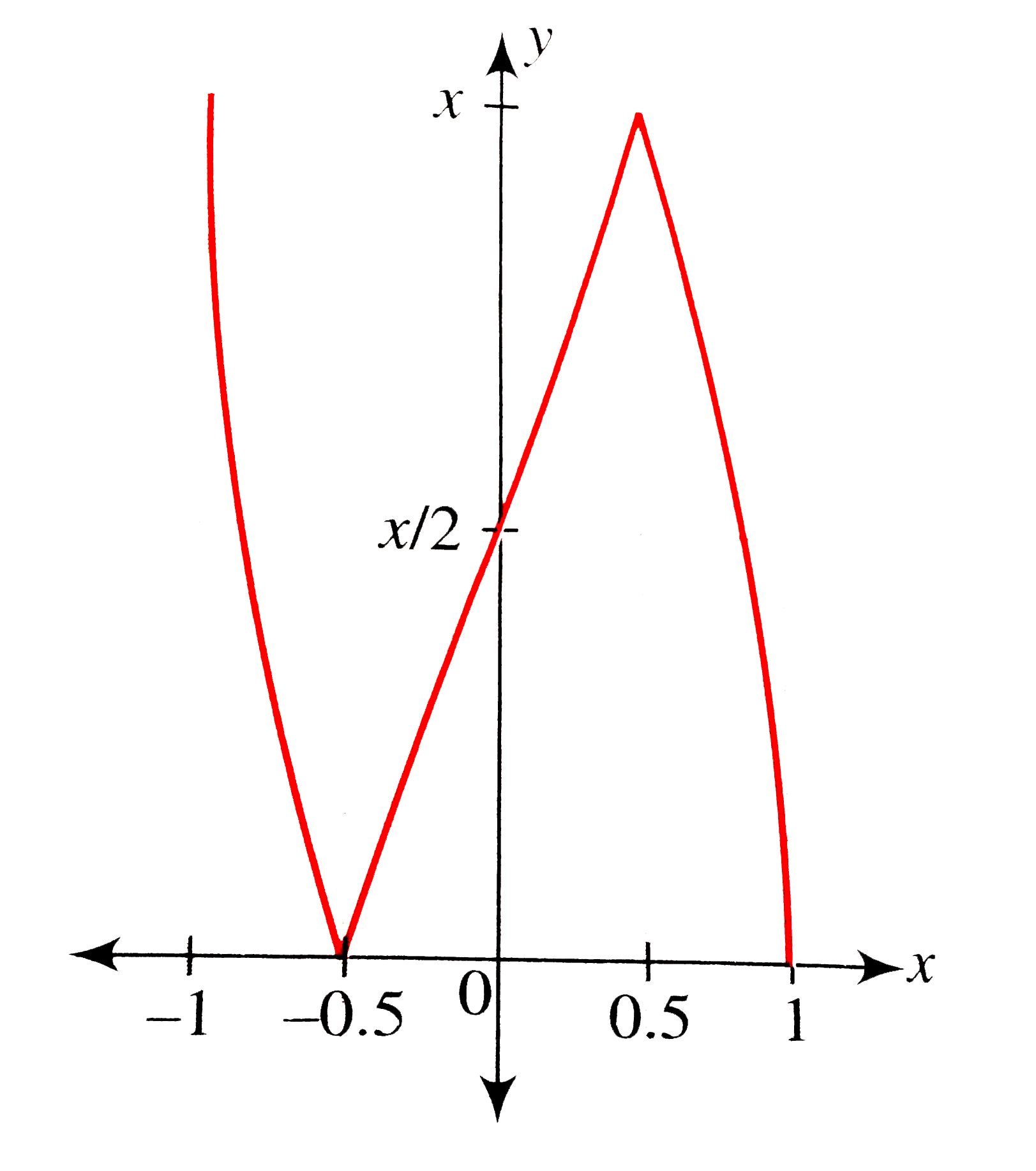
|
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHICAL TRANSFORMATIONSBook:CENGAGEChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
Similar Questions
Draw the graph of f(x)=x2−3
View SolutionDraw the graph of y=x3/5
View SolutionDraw the graph of y=1−x21+x2 and hence draw the graph of y=cos−1.1−x21+x2.
View SolutionDraw the graph of f(x)=x|x|.
View SolutionDraw the graph of y=loge(x3−x)
View SolutionDraw the graph of f(x)=sgn(x3−x).
View SolutionDraw the graph of y=sin3x.
View SolutionDraw the graph of y=cos−1x3 and compare with the graph of y=cos−1x.
View SolutionDraw the graph of y=3x−x31−3x2 and hence the graph of y=tan−1.3x−x31−3x2.
View SolutionDraw the graph of f(x)=x3−xx2−1.
View Solution

