A man runs along a straight road. Naturally he leans a little in the forward direction. The angle with the horizontal line and the line joining the man's centre of mass with the point of support is α ( assume mass per unit length of the man is uniform ) . The man will not slip if the coefficient of friction μ satisfies the conditon.
μ>cotα
μ<cotα
μ>tanα
μ<tanα
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the man as he runs and leans forward. The goal is to find the condition under which the man will not slip, in terms of the coefficient of friction (μ) and the angle (α).
1. Identify the Forces Acting on the Man:
- The gravitational force (weight) acting downwards: mg
- The normal force (N) acting upwards from the ground
- The frictional force (F_f) acting horizontally, preventing slipping
2. Balance the Vertical Forces:
- In the vertical direction, the forces must balance. Thus, we have:
N=mg
- This equation states that the normal force is equal to the weight of the man.
3. Determine the Frictional Force:
- The maximum frictional force can be expressed as:
Ff=μN
- Substituting the expression for normal force, we get:
Ff=μmg
4. Analyze the Torque about the Center of Mass:
- The torque due to the frictional force about the center of mass must be balanced by the torque due to the normal force.
- The torque due to friction (which tries to rotate the man anti-clockwise) is:
τf=Ff⋅Lsin(α)
- The torque due to the normal force (which tries to rotate the man clockwise) is:
τN=N⋅Lcos(α)
5. Set Up the Torque Balance Equation:
- For the man to not slip, the torques must balance:
Ff⋅Lsin(α)=N⋅Lcos(α)
- Canceling L from both sides gives:
Ffsin(α)=Ncos(α)
6. Substituting the Expressions for Forces:
- Substitute Ff=μmg and N=mg:
μmgsin(α)=mgcos(α)
- Dividing both sides by mg (assuming mg≠0):
μsin(α)=cos(α)
7. Rearranging the Equation:
- Rearranging gives:
μ=cos(α)sin(α)=cot(α)
8. Final Condition for No Slipping:
- Therefore, the condition for the man not to slip is:
cot(α)≤μ
Conclusion:
The man will not slip if the coefficient of friction μ satisfies the condition:
cot(α)≤μ
- The gravitational force (weight) acting downwards: mg
- The normal force (N) acting upwards from the ground
- The frictional force (F_f) acting horizontally, preventing slipping
- In the vertical direction, the forces must balance. Thus, we have:
N=mg
- This equation states that the normal force is equal to the weight of the man.
- The maximum frictional force can be expressed as:
Ff=μN
- Substituting the expression for normal force, we get:
Ff=μmg
- The torque due to the frictional force about the center of mass must be balanced by the torque due to the normal force.
- The torque due to friction (which tries to rotate the man anti-clockwise) is:
τf=Ff⋅Lsin(α)
- The torque due to the normal force (which tries to rotate the man clockwise) is:
τN=N⋅Lcos(α)
- For the man to not slip, the torques must balance:
Ff⋅Lsin(α)=N⋅Lcos(α)
- Canceling L from both sides gives:
Ffsin(α)=Ncos(α)
- Substitute Ff=μmg and N=mg:
μmgsin(α)=mgcos(α)
- Dividing both sides by mg (assuming mg≠0):
μsin(α)=cos(α)
- Rearranging gives:
μ=cos(α)sin(α)=cot(α)
- Therefore, the condition for the man not to slip is:
cot(α)≤μ
The man will not slip if the coefficient of friction μ satisfies the condition:
cot(α)≤μ
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )
33 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION(II) : MCQ ( SINGLE CORRECT)
47 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A uniform rod of length 2a is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance a/3 from the edge. The rod is released from rest. If the rod slips after it turned an angle θ, find the coefficient of friction between the rod and the table.
View SolutionA man is running along a road with speed u. On his chest there is a paper of mass m and area S. There is a wind blowing against the man at speed V. Density of air is ρ. Assume that the air molecules after striking the paper come to rest relative to the man. Find the minimum coefficient of friction between the paper and the chest so that the paper does not fall ?
View Solution
Knowledge Check
A man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
Auˆi−utanθˆjBuˆi−ucotθˆjCuˆi+ucotθˆjDutanθˆi−uˆjA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
Aui-ujBuˆi−utanθˆjC2uˆi+ucotθˆjDui+usinθˆjThe end of a heavy uniform rod AB can slide along a rough horizontal rod AC to which it is attached by a ring. B and C are joined by a string. If ABC be a right angle, when the rod is on the point of sliding, μ the coefficient of friction and α the angle between AB and the vertical, then
Aμ=2tanα/(2+tan2α)Bμ=tanα/(2+tan2α)Cμ=2cotα/(1+cot2α)Dμ=cotα/(2+cot2α)
A 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
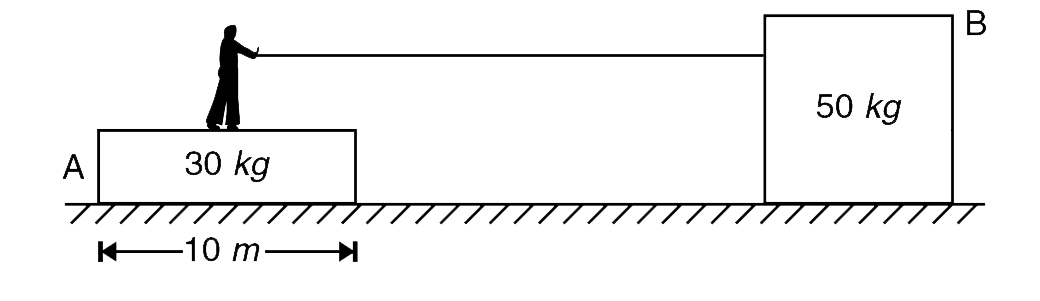
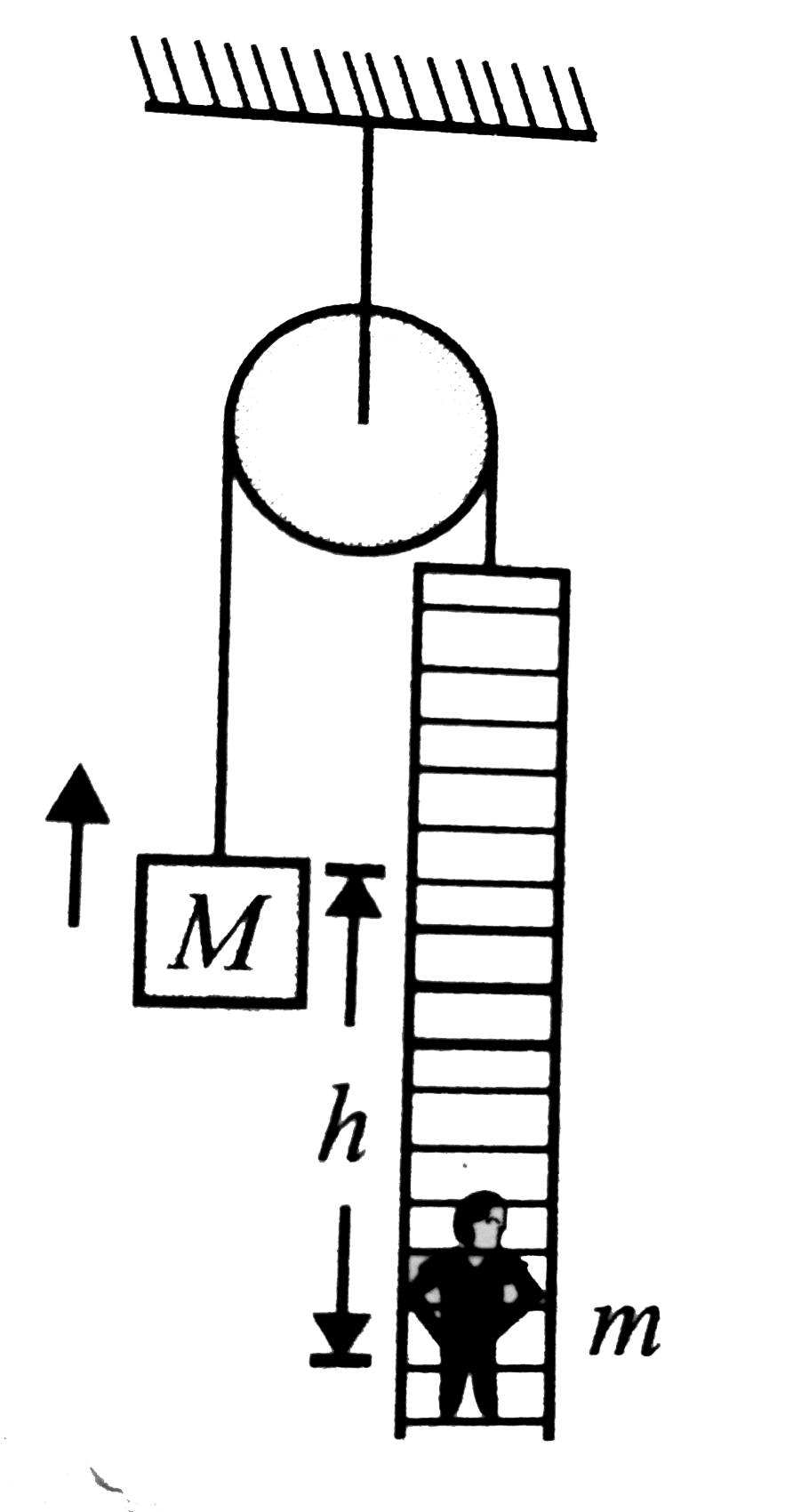
View SolutionA stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass M. Mass of the man is m. initially, the centre of mass of the counterweight is at a height h from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
View SolutionA thin rod of mass m and length 2l is placed horizontally and perpendicular to a horizontal rough nail, as shown in figure and set free. The point of contanct of the rod with the nails is l/3 distance away form the centre of rod. If the rod starts slipping when it forms an angle θ with the horizontal and the coefficient of friction of rod with nails is μ, then find μtanθ.

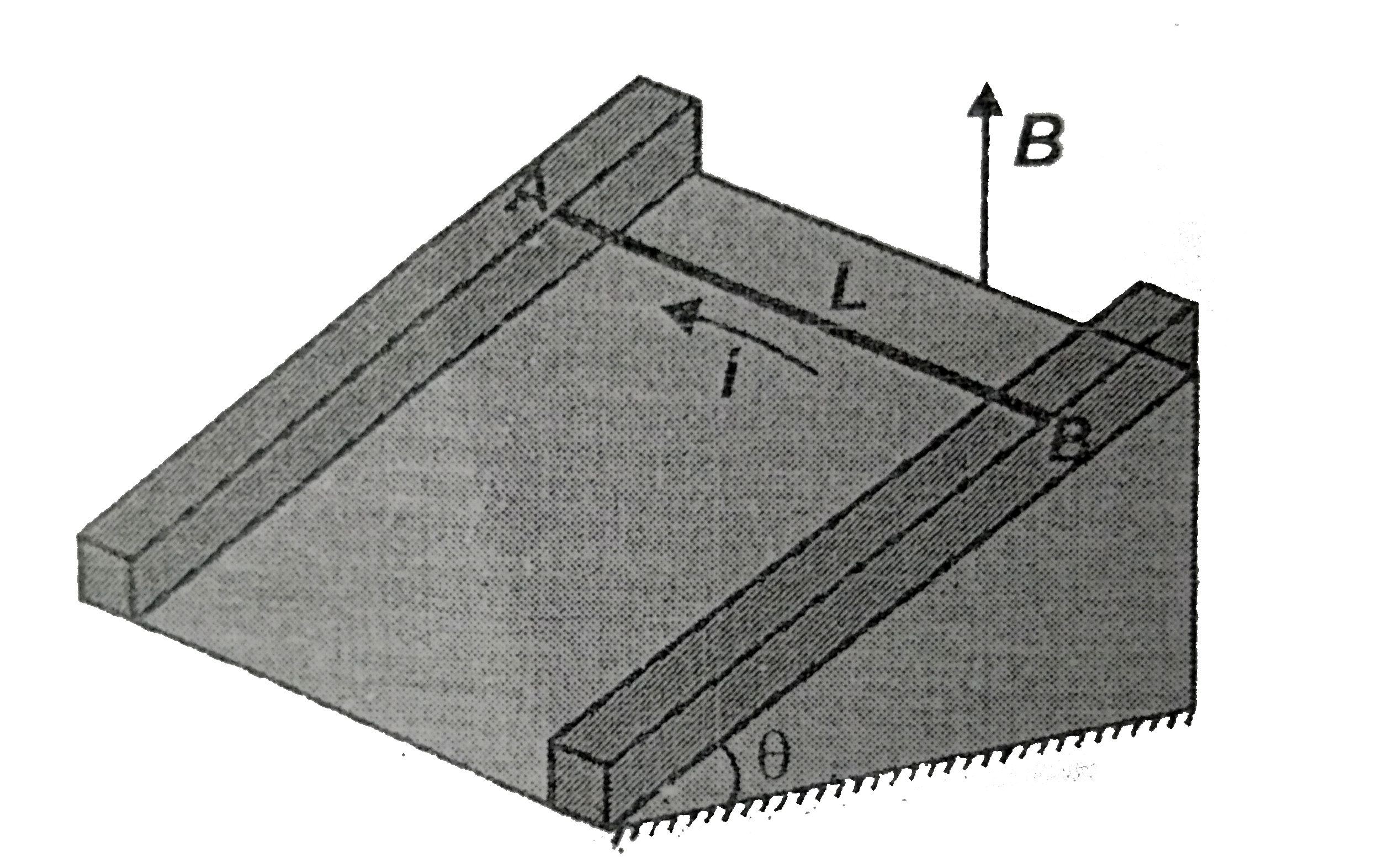
View SolutionOn an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
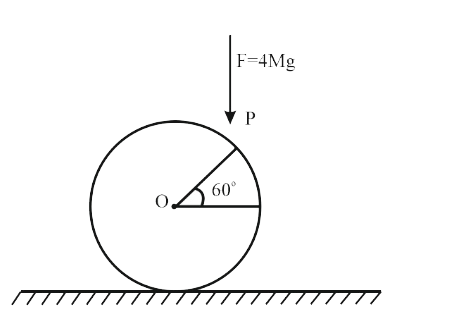
View SolutionA uniform solid sphere of mass M and radius R is lying on a rough horizonal plane. A constant force F=4Mg acts vertically downwards at point P such that the line OP makes an angle of 60∘ with the horizontal as shown in the figure. The minimum value of the coefficient of friction μ so that sphere performs pure rolling, is
View Solution
