In one dimentional collision between two idential particles 'A' and 'B'. 'B' is stationary and 'A' has momentum 54 kg-m/ sec before impact. During impact , 'B' gives an impulse 3kg-m/sec to 'A' . The coefficient of restitution between A and B is
2/5
1/5
1/2
3/5
The correct Answer is:B
To find the coefficient of restitution (e) between two identical particles A and B during a one-dimensional collision, we can follow these steps:
1. Identify Initial Conditions:
- Particle A has an initial momentum PA=54kg m/s.
- Particle B is stationary, so its initial momentum PB=0kg m/s.
2. Impulse Given:
- During the collision, particle B gives an impulse J=3kg m/s to particle A.
3. Calculate Final Momentum of A:
- The final momentum of A after receiving the impulse can be calculated as:
PA,final=PA+J=54kg m/s+3kg m/s=57kg m/s
4. Calculate Final Momentum of B:
- Since both particles are identical, let their mass be m. The impulse given to A will result in an equal and opposite impulse on B. Thus, the final momentum of B is:
PB,final=J=3kg m/s
5. Calculate Velocities:
- The velocity of A after the collision can be calculated using its final momentum:
VA=PA,finalm=57mm/s
- The velocity of B after the collision is:
VB=PB,finalm=3mm/s
6. Calculate Velocity of Separation and Velocity of Approach:
- The velocity of separation (after collision) is given by:
Vseparation=VB−VA=3m−57m=3−57m=−54mm/s
- The velocity of approach (before collision) is:
Vapproach=54mm/s
7. Calculate Coefficient of Restitution:
- The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach:
e=|Vseparation||Vapproach|=∣∣−54m∣∣∣∣54m∣∣=54/m54/m=1
Final Answer:
The coefficient of restitution e between particles A and B is 89.
- Particle A has an initial momentum PA=54kg m/s.
- Particle B is stationary, so its initial momentum PB=0kg m/s.
- During the collision, particle B gives an impulse J=3kg m/s to particle A.
- The final momentum of A after receiving the impulse can be calculated as:
PA,final=PA+J=54kg m/s+3kg m/s=57kg m/s
- Since both particles are identical, let their mass be m. The impulse given to A will result in an equal and opposite impulse on B. Thus, the final momentum of B is:
PB,final=J=3kg m/s
- The velocity of A after the collision can be calculated using its final momentum:
VA=PA,finalm=57mm/s
- The velocity of B after the collision is:
VB=PB,finalm=3mm/s
- The velocity of separation (after collision) is given by:
Vseparation=VB−VA=3m−57m=3−57m=−54mm/s
- The velocity of approach (before collision) is:
Vapproach=54mm/s
- The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach:
e=|Vseparation||Vapproach|=∣∣−54m∣∣∣∣54m∣∣=54/m54/m=1
The coefficient of restitution e between particles A and B is 89.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )
33 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION(II) : MCQ ( SINGLE CORRECT)
47 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
In a one-dimensional collision between two identical particles. A and B, B is stationary and A has momentum p before impact. During impact, B gives an impulse J to A. Find the coefficient of restitution between A and B?
View SolutionA sphere A of mass m, travelling with speed v, collides directly with a stationary sphere B. If A is brought to rest and B is given a speed V, find (a) the mass of B (b) the coefficient of restitution between A and B?
View Solution
Knowledge Check
In a one dimensional collision between two identical particles A and B, B is stationary and A has momentum p before impact. During impact, B given J to A.
AThe total momentum of the A+B System is p before and after impact, and (p−1) during the impact.BDuring the impact A given impulse J to BCthe coefficient of restituation is 2Jp−1DThe coefficient of restituation is Jp+1In one-dimensional collision between two identical particles A and B,B is stationary and A has momentum p before and after the impact, and(P-J) during the impact:
Athe total momentum of the A plus B, system is P before and after the impact and (P-J) during the impact.BDuring the impact A gives impules J to BCthe coefficient of restitution is 2JP−1Dthe coefficient of restitution is JP+1In a head on collision between tow identical particles A and B moving on a horizontal surface, B is stationary and A has momentium P0 before impact. Due to the impact, A recieives an inpulse I. Then coefficient of restitution between the two is :
A2IP0−1B2IP0+1CIP0+1DIP0−1
Two smooth spheres. A and B. having equal radii, lie on a horizontal table. A is of mass m and B is of mass 3m. The spheres are projected towards each other with velocity vector 5ˆi+2ˆj and 2ˆi−ˆj, respectively, and when they collide the lige joining their centres is parallel to the vector ˆi. If the coefficient of restitution between A and B is 1/3, find the velocities after impact and the loss in kinetic energy caused by the collision. Find also the magnitude of the impulses that act at the instant of impact.
View SolutionIn head - on collision between two particles A and B of same mass , A is moving with momentum 15kgm/s , B is stationary . During the impact , B gives impulse 10N−s to A . The coefficient of restitution is
View SolutionA body X with a momentum p collides with another identical stationary body Y one dimensionally. During the collision, Y gives an impulse J to body X. Then coefficient of restitution is
View SolutionBlock A has mass 40kg and B has 15kg and F is 500N parallel to smooth inclined plane.The system is moving together

The least coefficient of friction between A and B is
View SolutionTwo equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
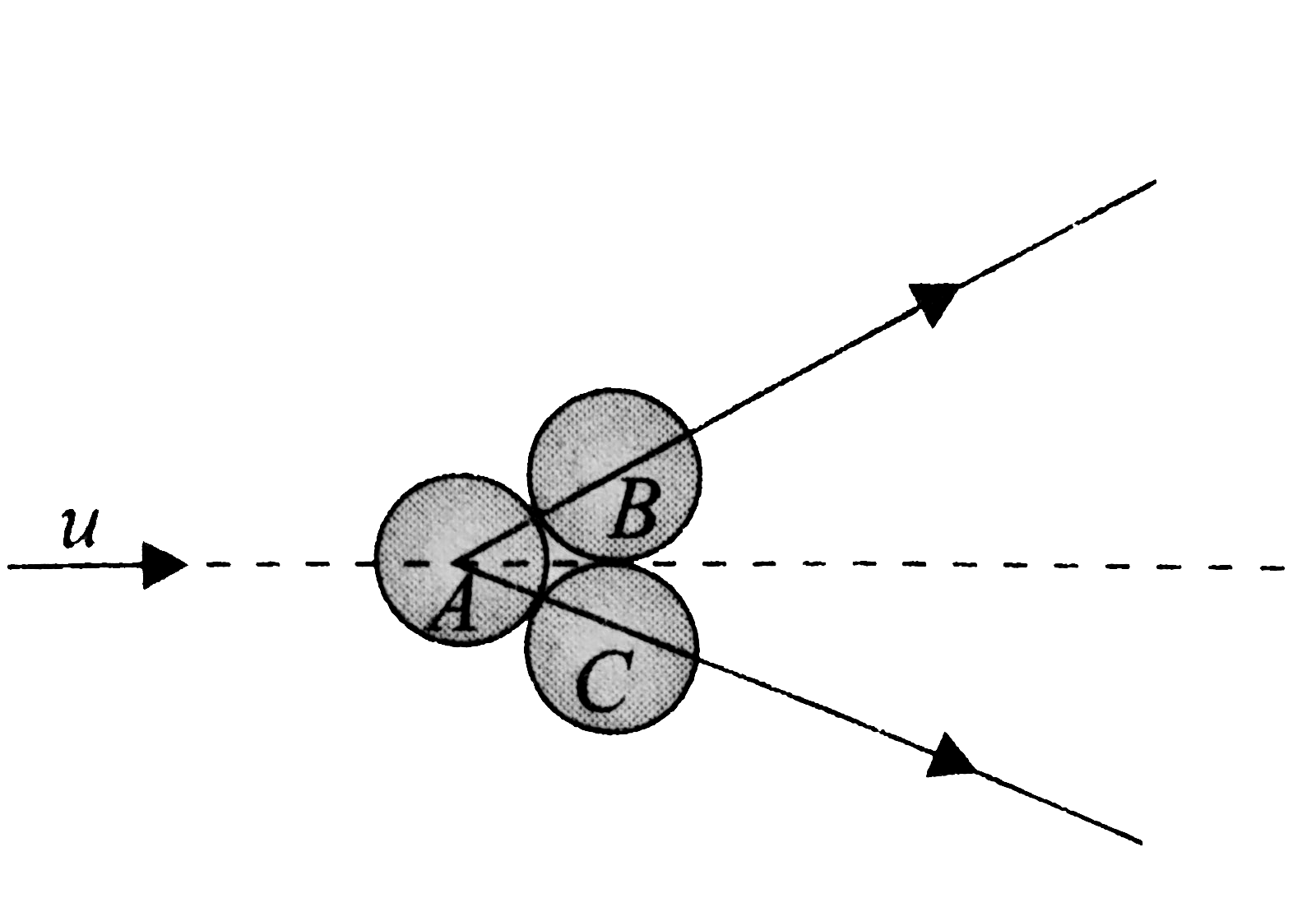
The coefficient of restitution between the two spheres A and B (or between A and C) is
View Solution
