A particle is moving in a circle of radius 23m and mass of the particle is 2kg. The kinetic energy of the particle dependes on distance 'S' travelled by the particle as K.E. = 4S4. The angle made by net acceleration with the radial acceleration when the particle rotate by 60∘ is
tan−1(3π)
tan−1(6π)
tan−1(1π)
tan−1(4π)
The correct Answer is:B
To solve the problem, we need to find the angle made by the net acceleration with the radial acceleration when the particle rotates by 60∘. We will follow these steps:
Step 1: Understand the given data
- Radius of the circle, R=23m
- Mass of the particle, m=2kg
- Kinetic energy as a function of distance S:
K.E.=4S4
Step 2: Find the expression for velocity
The kinetic energy can also be expressed as:
K.E.=12mv2
Equating the two expressions for kinetic energy:
12mv2=4S4
Substituting m=2:
12⋅2⋅v2=4S4⟹v2=8S4
Step 3: Find radial acceleration Ac
The centripetal (radial) acceleration is given by:
Ac=v2R
Substituting v2=8S4 and R=23:
Ac=8S423=12S4
Step 4: Find tangential acceleration At
The tangential acceleration can be found from the change in velocity. We know:
At=d(v2)dt⋅12v
To find d(v2)dt, we can use:
v2=8S4⟹d(v2)dt=32S3⋅dSdt
Since dSdt=v, we have:
At=32S3⋅v2v=16S3
Step 5: Calculate the angle α
The net acceleration Anet can be found using the Pythagorean theorem:
Anet=√A2c+A2t
The angle α made by the net acceleration with the radial acceleration is given by:
tan(α)=AtAc
Substituting the values:
tan(α)=16S312S4=43S
Step 6: Find S when the particle has rotated 60∘
The distance S traveled when the particle rotates by 60∘ is given by:
S=R⋅θ=23⋅π3=2π9
Step 7: Substitute S into the angle equation
Substituting S=2π9:
tan(α)=43⋅2π9=4⋅96π=6π
Step 8: Find α
Thus, the angle α is:
α=tan−1(6π)
Final Answer
The angle made by the net acceleration with the radial acceleration when the particle rotates by 60∘ is:
α=tan−1(6π)
- Radius of the circle, R=23m
- Mass of the particle, m=2kg
- Kinetic energy as a function of distance S:
K.E.=4S4
The kinetic energy can also be expressed as:
K.E.=12mv2
Equating the two expressions for kinetic energy:
12mv2=4S4
Substituting m=2:
12⋅2⋅v2=4S4⟹v2=8S4
The centripetal (radial) acceleration is given by:
Ac=v2R
Substituting v2=8S4 and R=23:
Ac=8S423=12S4
The tangential acceleration can be found from the change in velocity. We know:
At=d(v2)dt⋅12v
To find d(v2)dt, we can use:
v2=8S4⟹d(v2)dt=32S3⋅dSdt
Since dSdt=v, we have:
At=32S3⋅v2v=16S3
The net acceleration Anet can be found using the Pythagorean theorem:
Anet=√A2c+A2t
The angle α made by the net acceleration with the radial acceleration is given by:
tan(α)=AtAc
Substituting the values:
tan(α)=16S312S4=43S
The distance S traveled when the particle rotates by 60∘ is given by:
S=R⋅θ=23⋅π3=2π9
Substituting S=2π9:
tan(α)=43⋅2π9=4⋅96π=6π
Thus, the angle α is:
α=tan−1(6π)
The angle made by the net acceleration with the radial acceleration when the particle rotates by 60∘ is:
α=tan−1(6π)
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION (II) : (SUBJECTIVE )
Explore 33 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION(II) : MCQ ( SINGLE CORRECT)
Explore 47 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS
Explore 3 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
A particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View Solution
Knowledge Check
A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
A25ms−2B36ms−2C5ms−2D15ms−2A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
A25m/s2B36m/s2C5m/s2D15m/s2A particle moves in a circle of radius 5 cm with constant speed and time period 0.2π. The acceleration of the particle is:
A15m/s2B25m/s2C36m/s2D5m/s2
A particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View SolutionA particle moves in a circle of radius 25 cm at two revolutions per sec. The acceleration of the particle in m/s2 is:
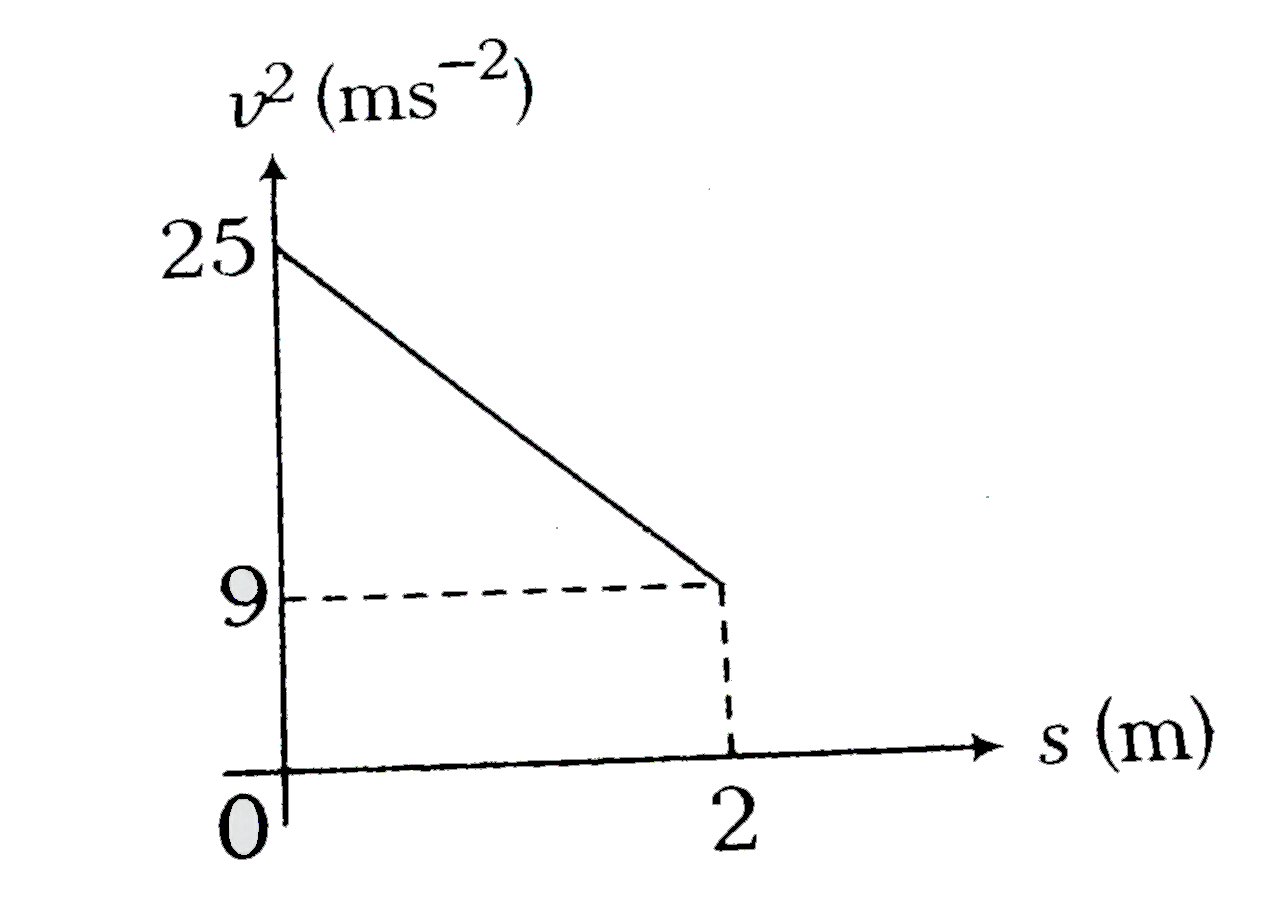
View SolutionA graph between the square of the velocity of a particle and the distance s moved by the particle is shown in the figure. The acceleration of the particle is
View SolutionIf KE of the particle of mass m performing UCM in a circle of radius r is E. Find the acceleration of the particle
View Solution

