A particle is projected horizontally with a speed v0 at t = 0 from a certain point above the ground . What is the magnitude of tangential acceleration of the particle at t=t1 is ( Assume that the particle does not strike the ground between the time interval t = 0 to t=t1 )
gt√v20+g2+2
tg2√v20+g2t2
tg√v20+g2t2
gt√g+v20t
The correct Answer is:B
To solve the problem, we need to find the magnitude of the tangential acceleration of a particle projected horizontally with an initial speed v0 at time t=0. We will analyze the motion of the particle in both horizontal and vertical directions.
1. Understanding the Motion:
- The particle is projected horizontally, which means its initial vertical velocity uy=0.
- The horizontal velocity ux=v0 remains constant since there is no horizontal acceleration.
2. Vertical Motion:
- The only force acting on the particle in the vertical direction is gravity. Thus, the vertical acceleration ay=g (where g is the acceleration due to gravity).
- The vertical velocity vy at time t can be calculated using the equation of motion:
vy=uy+ayt=0+gt=gt
3. Horizontal Motion:
- The horizontal velocity remains constant:
vx=v0
4. Resultant Velocity:
- At time t, the resultant velocity v of the particle can be found using the Pythagorean theorem:
v=√v2x+v2y=√(v0)2+(gt)2
5. Tangential Acceleration:
- The tangential acceleration is defined as the rate of change of the magnitude of the velocity. Since the horizontal component vx is constant and only the vertical component vy is changing, we can find the tangential acceleration at as follows:
- The magnitude of the tangential acceleration is given by:
at=d|v|dt
- To find d|v|dt, we differentiate v:
v=√(v0)2+(gt)2
- Using the chain rule:
d|v|dt=12√(v0)2+(gt)2⋅(2gt)=gt√(v0)2+(gt)2
6. Final Expression:
- Therefore, the magnitude of the tangential acceleration at time t=t1 is:
at=gt1√(v0)2+(gt1)2
Summary:
The magnitude of the tangential acceleration of the particle at time t=t1 is given by:
at=gt1√(v0)2+(gt1)2
- The particle is projected horizontally, which means its initial vertical velocity uy=0.
- The horizontal velocity ux=v0 remains constant since there is no horizontal acceleration.
- The only force acting on the particle in the vertical direction is gravity. Thus, the vertical acceleration ay=g (where g is the acceleration due to gravity).
- The vertical velocity vy at time t can be calculated using the equation of motion:
vy=uy+ayt=0+gt=gt
- The horizontal velocity remains constant:
vx=v0
- At time t, the resultant velocity v of the particle can be found using the Pythagorean theorem:
v=√v2x+v2y=√(v0)2+(gt)2
- The tangential acceleration is defined as the rate of change of the magnitude of the velocity. Since the horizontal component vx is constant and only the vertical component vy is changing, we can find the tangential acceleration at as follows:
- The magnitude of the tangential acceleration is given by:
at=d|v|dt
- To find d|v|dt, we differentiate v:
v=√(v0)2+(gt)2
- Using the chain rule:
d|v|dt=12√(v0)2+(gt)2⋅(2gt)=gt√(v0)2+(gt)2
- Therefore, the magnitude of the tangential acceleration at time t=t1 is:
at=gt1√(v0)2+(gt1)2
The magnitude of the tangential acceleration of the particle at time t=t1 is given by:
at=gt1√(v0)2+(gt1)2
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )
33 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION(II) : MCQ ( SINGLE CORRECT)
47 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
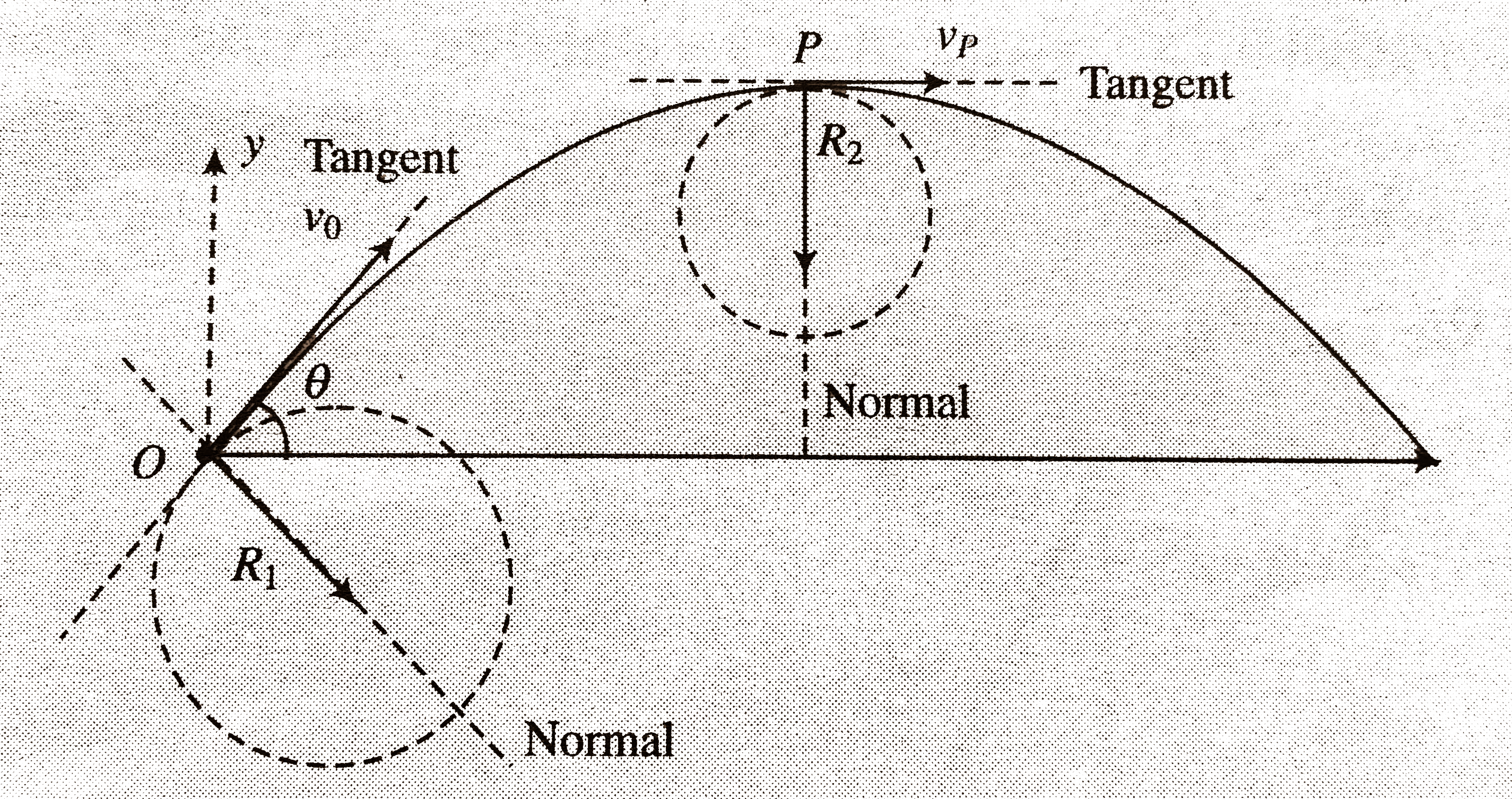
A particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionThe magnitude of displacement (in meters) by the particle from time t = 0 to t = t will be –
View Solution
Knowledge Check
Starting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
AAt t=2s, the position of the particle is at x=9mBParticle acceleration at t=2s is 1m/s2CParticle acceleration is 1/2m/s2 through out the motionDParticle will never go in negative direction from it's starting positionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
Ag2sin2θu2B2g2sinθu2Cg2sinθu2Dg2sin2θ2u2Two particles are projected horizontally with same speed 30m/s but in opposite directions from same height at time t=0. Calculate angle between velocity vectors of particles at time t=3s.
A0∘B30∘C60∘D90∘
A particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
View SolutionA particle is projected at time t=0 from a point P wilth a speed v0 at an angle of 45∘ to the horizontal. Find the magnitude and the direction of the angular momentum of the parallel about the point P at time t=v0g
View SolutionA particle of mass m is projected at t=0 from the point P on the ground with speed v0 at an angle of θ to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time t=v0sinθ2g.
View SolutionA particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA particle is projected from ground with speed 80 m/s at an angle 30∘ with horizontal from ground. The magnitude of average velocity of particle in time interval t = 2 s to t = 6 s is [Take g = 10 m/s2]
View Solution
