The bob hanging from a light string is projected horizontally with a speed u0. In the subsequent upward motion of the bob in vertically plane

A negative amount of work has been done by tension on the bob.
A positive amount of work has been done by gravity on the bob.
The tension in the string and speed of bob both may become zero at an instant.
none of these
The correct Answer is:C
Step by step video, text & image solution for The bob hanging from a light string is projected horizontally with a speed u_(0). In the subsequent upward motion of the bob in vertically plane by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION (II) : (SUBJECTIVE )
Explore 33 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION(II) : MCQ ( SINGLE CORRECT)
Explore 47 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS
Explore 3 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionBob of a simple pendulum of length L is projected horizontally with a speed of u=√4gh, , from the lowest position. Find the distance of the bob from vertical line AB, at the moment its tangential acceleration becomes zero.
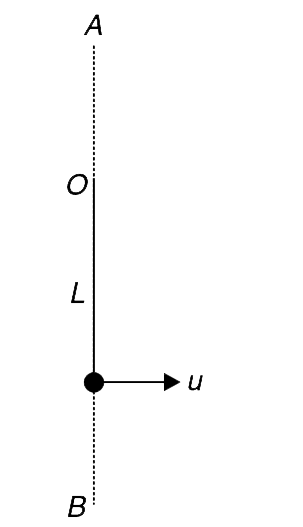
View Solution
Knowledge Check
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
A√glB√2glC√3glD√gl3A particle is projected vertically upwards in vacuum with a speed u.
AWhen it rises to half its maximum height, its speed becomes u/2.BWhen it rises to half its maximum height, its speed becomes u/√2.CThe time taken to rise to half its maximum height is half the time taken to reach its maximum height.DThe time taken to rise to three− fourth of its maximum height is half the time taken to reach its maximum height.
A simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u=√(2+√3)ag . The angle with the downward vertical, string makes where string becomes slack is :
View SolutionA pendulum bob swing from the point P when the ideal string of length l is horizontal. Find the
(A) Speed
(B) Acceleration of the bob
(C ) Power delivered by gravity at an angular position θ
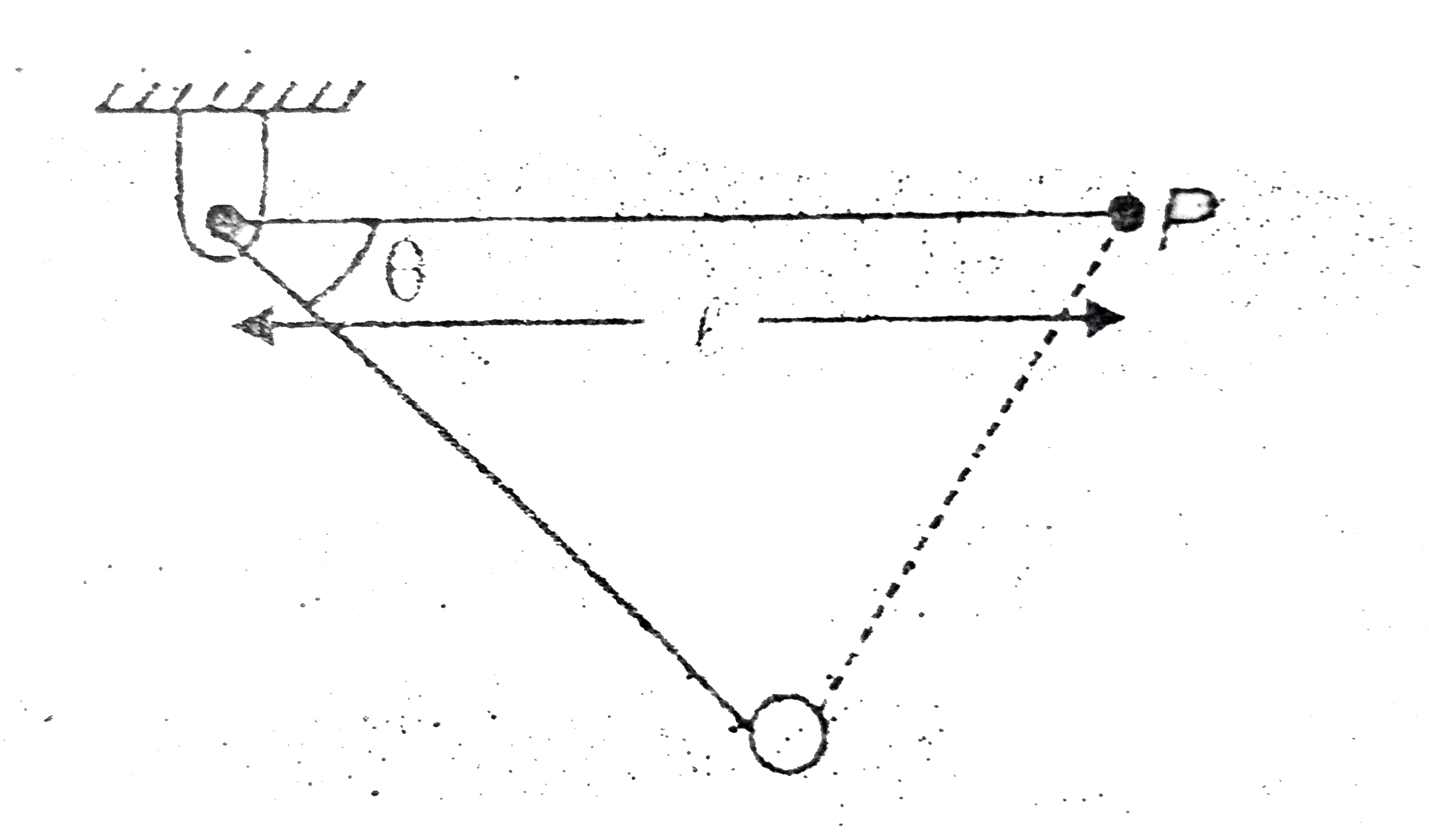
View SolutionThe bob of a simple pendulum of length 1m hangs at rest. It is suddenly projected horizontally with velocity 10ms−1. Calculate the velocity of the bob and tension of the string when it is horizontal. The mass of the bob is 12kg.
[Hint : See worked out example 4]
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View Solution

