In the figure shown a monkey of mass m is standing on a ladder of mass ( M -m ) . On the other side of th elight pulley hangs a counter weight of mass M as shown. The whole system is stationary. Now the monkey starts moving up the ladder. In the process, The center of mass of the shole system :
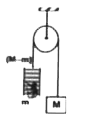
moves down
moves up
remains stationary
nothing can be concluded in general
The correct Answer is:B
Step by step video, text & image solution for In the figure shown a monkey of mass m is standing on a ladder of mass ( M -m ) . On the other side of th elight pulley hangs a counter weight of mass M as shown. The whole system is stationary. Now the monkey starts moving up the ladder. In the process, The center of mass of the shole system : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION (II) : (SUBJECTIVE )
Explore 33 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION(II) : MCQ ( SINGLE CORRECT)
Explore 47 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS
Explore 3 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
Knowledge Check
A balloon of mass M with a light rope having monkey on the rope is in equilibrium. If the monkey starts moving up with acceleration a w.r.t. rope . Then the acceleration of cenre of mass of the system is
 Aa(M−m)(M+m)BZeroCaDaMm
Aa(M−m)(M+m)BZeroCaDaMmIn the figure shown, a particle of small mass m is joined to a very heavy mass M (M >> m) by a light string passing over a light pulley. The total downward force on the pulley by the string is :
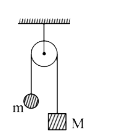 AmgB2 mgC4 mgD(M + m) g
AmgB2 mgC4 mgD(M + m) gThe velocity (in m/s) of centre of mass of the system as shown in the figure is :
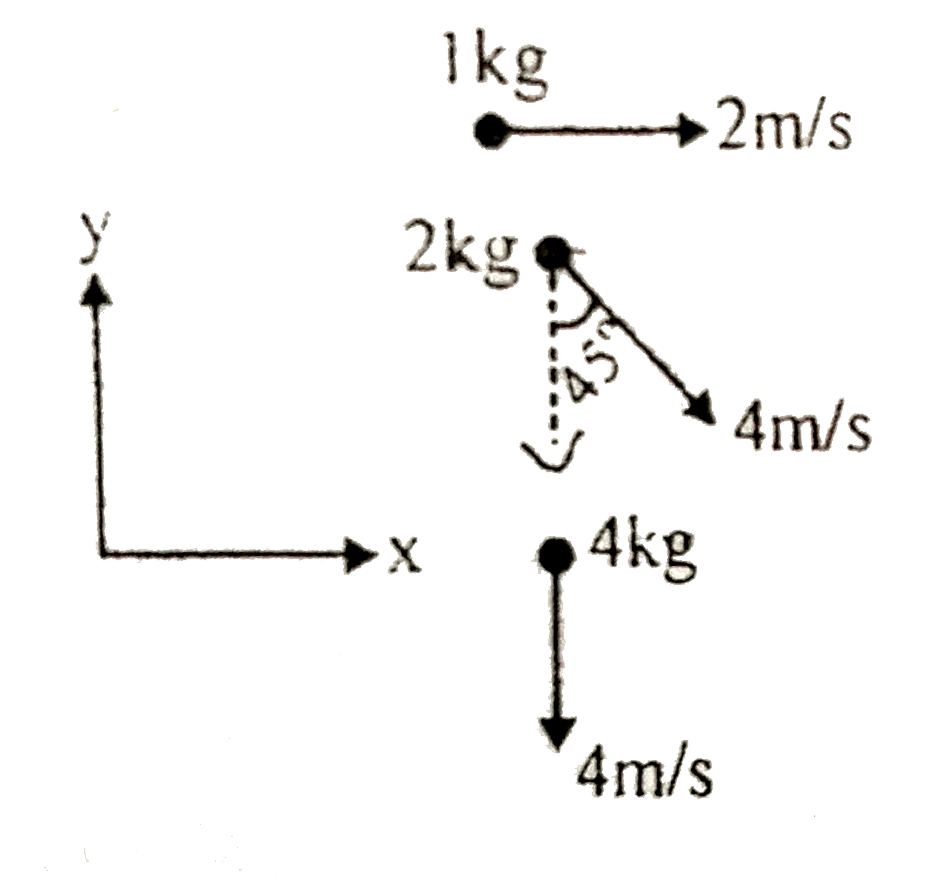 A2[1+4√2]ˆi+8[1√2+2]ˆj7B2[1+4√2]ˆi+8[1√2−2]ˆj7C2[1+4√2]ˆi−8[1√2+2]ˆj7D8[1√2−2]ˆi+2[1+4√2ˆj]7
A2[1+4√2]ˆi+8[1√2+2]ˆj7B2[1+4√2]ˆi+8[1√2−2]ˆj7C2[1+4√2]ˆi−8[1√2+2]ˆj7D8[1√2−2]ˆi+2[1+4√2ˆj]7
Two ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

View SolutionFigure shows 4 identical masses of mass m, arranged on a cube as shown.
The potential energy of the system is
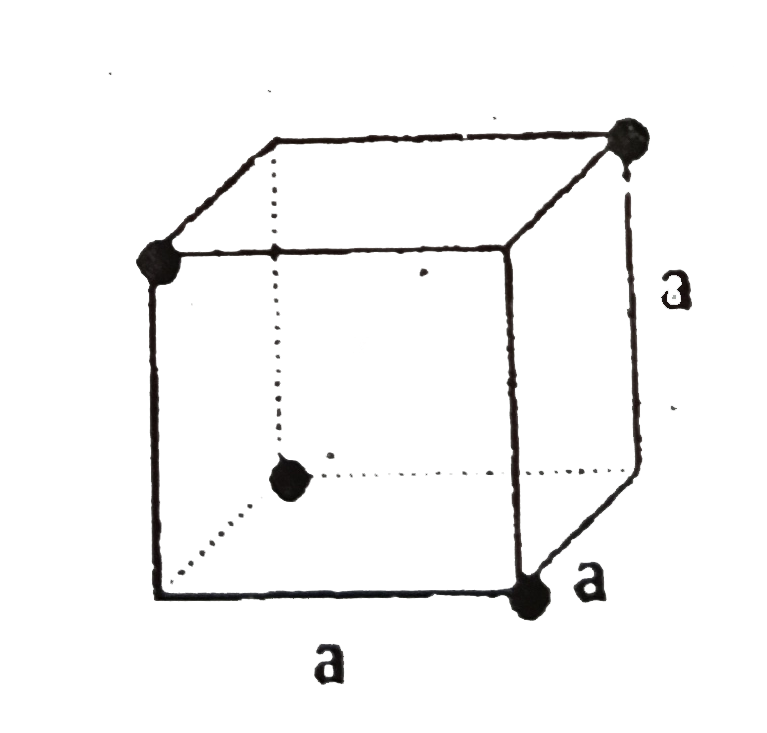
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View SolutionA stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l′ with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View Solution



