find out mass of the charge Q, so that it remains in equilibrium for the given configuration.
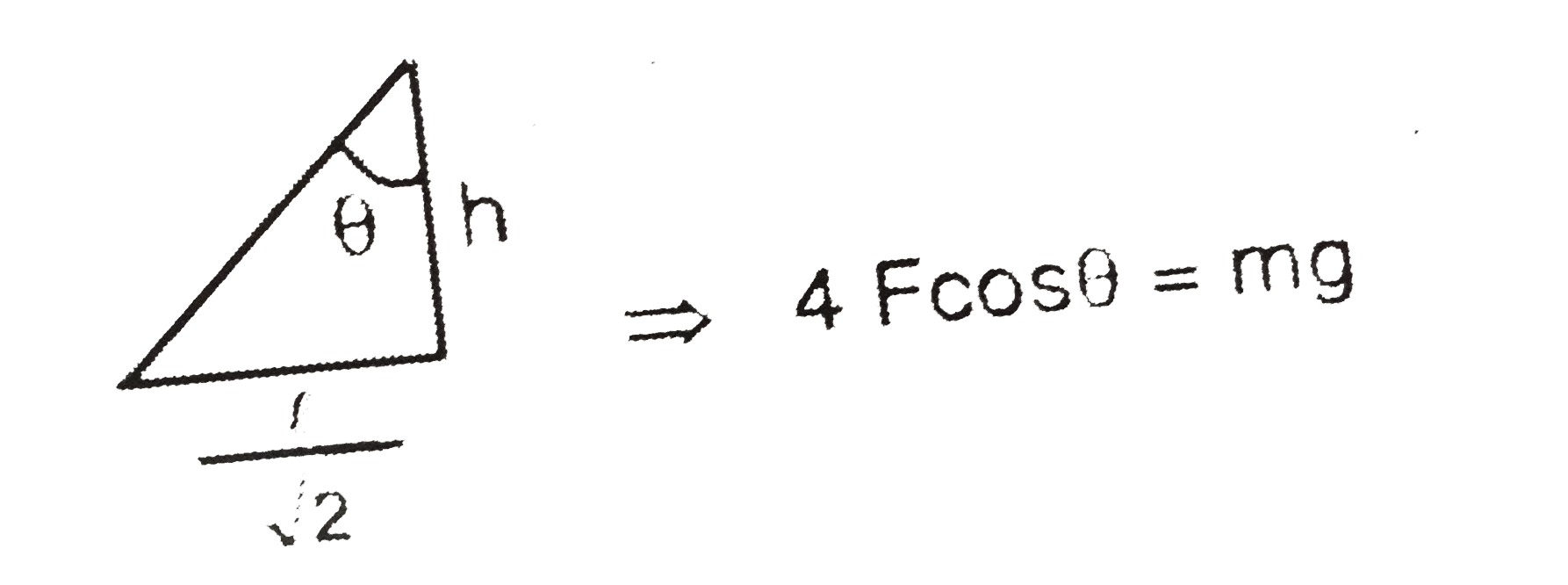
⇒4Fcosθ=mg
⇒4×KQq(l22+h2)3/2h=mg ∴m=4KQqhg(l22+h2)3/2

Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
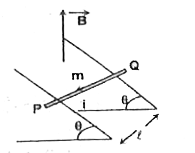
Find the current in the conductor PQ so that it remains in equilibrium under its own weight and the magnetic force. If direction of current is reversed then what would be initial acceleration of the rod? Mass of the rod is m. (Friction is assumed to be absent)
View Solution(a) Derive and expression for the electric field at any point on the equatorial line of an electric dipole.
(b) Two identical point charges, q each kept 2m apart in air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
View Solution
Knowledge Check
A charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:
A(a) Q2B(b) −Q2C(c) Q4D(d) −Q4Four charges equal to Q are placed at the four comers of a square and a charge q is at its centre . If the system is in equilibrium , the value of q is
A−Q4(1+2√2)BQ4(1+2√2)C−Q2(1+2√2)DQ2(1+2√2)Four charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
A(a) −Q2(1+2√2)B(b) Q4(1+2√2)C(c) −Q4(1+2√2)D(d) Q2(1+2√2)
Two identical point charges ,q each , are kept 2 m apart in air. A third pint charges Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
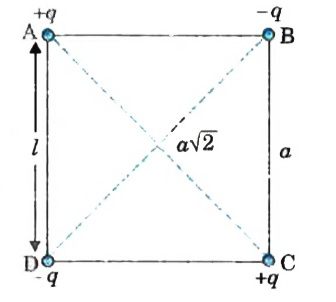
View SolutionTwo point charges of +q each are placed at two diagonally opposite corners of a square. Another two point charges of -q charge each are placed at the two remaining corners. Take the edge length of square equal to l. Calculate (i) work needed to move these charges slowly from an infinite separation to this given configuration. (ii) Assume that four charges at corners of the square are held fixed. Another charge Q is to be moved from infinity to the centre of this square slowly. What additional work is required to do so?
View Solution(a) Two point charges Q and 16Q are fixed at separation d. Where should a third point charge be placed between them so that it experiences no force I.e. in equilibrium ?
(b) In the previous problem , if we replace Q by −Q , where should the third charge be placed on the joining the charges so that it is equilibrium ?
(c ) Three point charges Q,q and Q are placed at x=0,x=d/2 and x=d. Find q in terms of Q so that all charges are in equilibrium.
(d) Two point charges 9Q and 25Q are placed at separation d. Where should a third charge q be placed between them so that all charges are in equilibrium ? Also find the value of q and its nature.
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre, If the system is in equilibrium the value of q si
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View Solution
