Two point charges of +q each are placed at two diagonally opposite corners of a square. Another two point charges of -q charge each are placed at the two remaining corners. Take the edge length of square equal to l. Calculate (i) work needed to move these charges slowly from an infinite separation to this given configuration. (ii) Assume that four charges at corners of the square are held fixed. Another charge Q is to be moved from infinity to the centre of this square slowly. What additional work is required to do so?

Video Solution

Text Solution

Verified by Experts

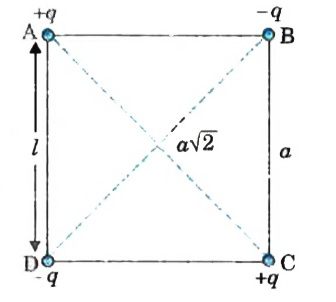
The given arrangement of charges is shown below:
(i) Work required to move these charges slowly from infinite separation to this given configuration will be equal to the difference in electric potential energy of the systems at this configuration and at infinite separation.
$∴ W = U - U_{\infty}$
We know that $U_{\infty} = 0$ and $U =$ Total electric potential energy of the four charges
$∴ W = U$
$= \frac{1}{4 π ε_{0}} [\frac{q_{A} q_{B}}{A B} + \frac{q_{A} q_{C}}{A C} + \frac{q_{A} q_{D}}{A D} + \frac{q_{B} q_{C}}{B C} + \frac{q_{C} q_{D}}{C D} + \frac{q_{B} q_{D}}{B D}]$
Here, $q_{A} = + q, q_{B} = - q, q_{c} = + q, q_{D} = - q$
$A B = B C = C D = A D = l$
$A C = B D = \sqrt{A D^{2} + D C^{2}} = \sqrt{2} l$
$\Rightarrow W = \frac{1}{4 π ε_{0}}$
$[\frac{- q^{2}}{l} + \frac{q^{2}}{\sqrt{2} l} + \frac{(- q^{2})}{l} + \frac{(- q^{2})}{l} + \frac{(- q^{2})}{l} + \frac{q^{2}}{\sqrt{2} l}]$
$= - \frac{q^{2}}{4 π ε_{0} l} (4 - \sqrt{2})$
(ii) To calculate the work required to move another charge Q from infinity to the centre of the square, we will first calculate the electrostatic potential energy of the system of charges when the charge Q is placed at the centre:
$U = \frac{1}{4 π ε_{0}} [\frac{q Q}{A O} - \frac{q Q}{B O} + \frac{q Q}{C O} - \frac{q Q}{D O}]$
Here, $A O = B O = C O = D O$
$∴ U = 0$
$∴$ Work done in bringing Q from infinity to centre, $W = U = 0$

Updated on:21/07/2023

Four charges $+ Q, - Q, + Q, - Q$ are placed at the corners of a square taken in order. At the centre of the square
A $E = 0, V = 0$
B $E = 0, V \neq 0$
C $E \neq 0, V = 0$
D $E = 0, V \neq 0$