Shows rod of mass and resistance moving on two fixed, resistanceless, smooth conducting rails (closed on both sides by resistances ). Find the current in the rod (at the instant its velocity is ).
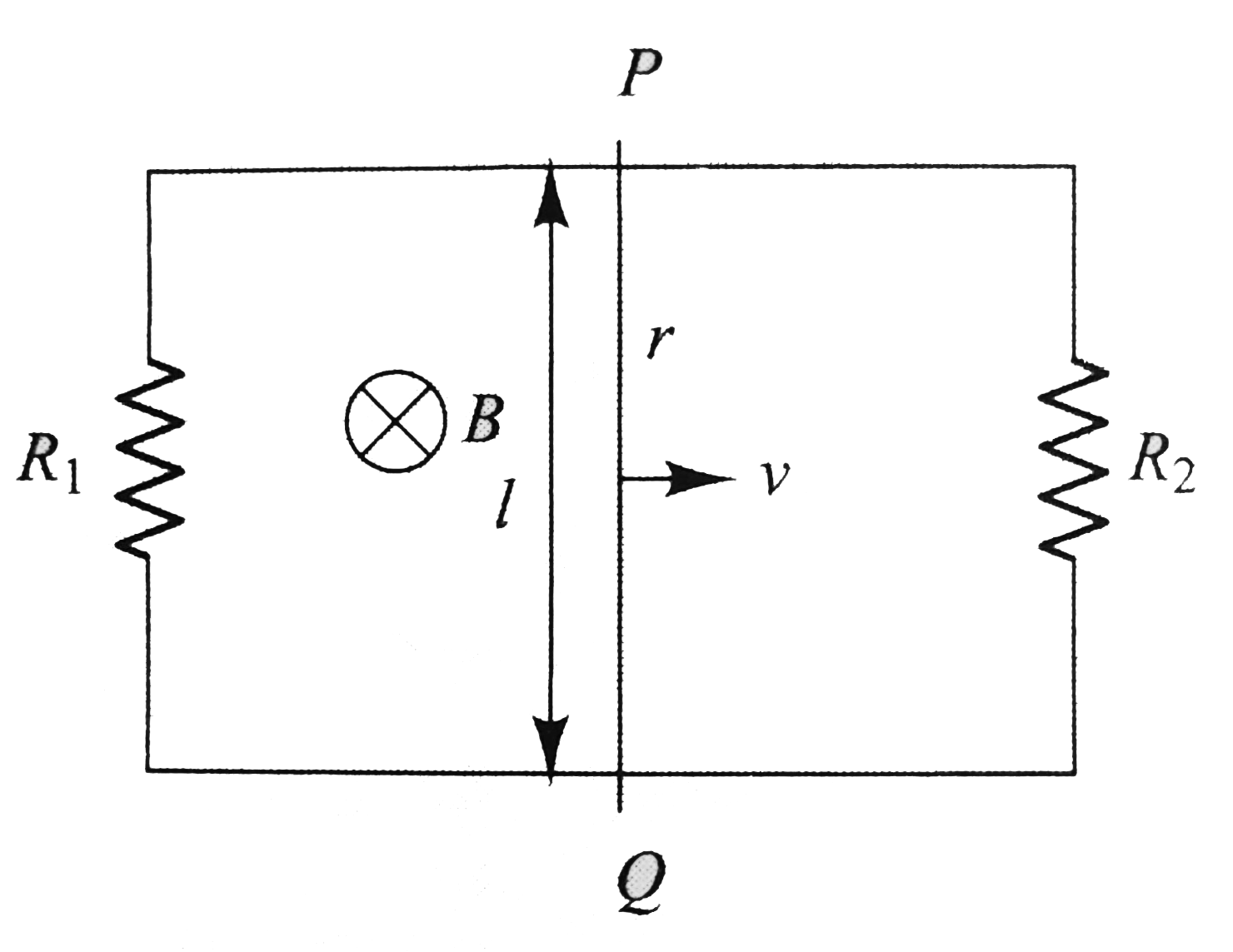
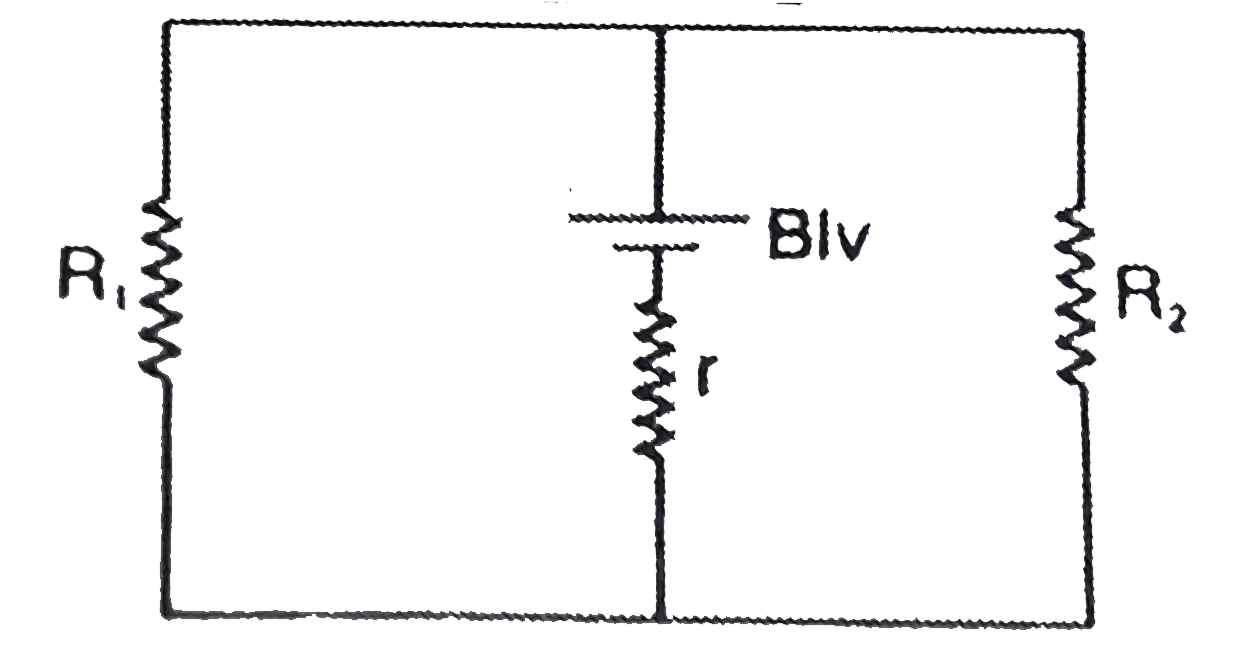
this circuit is equivalent to the following diagram .
Similar Questions
A rod of mass m and resistance r is placed on fixed, resistanceless, smooth conducting rails (closed by a resistance R) and it is projected with an initial velocity u.Find its velocity as a function of time.
 View Solution
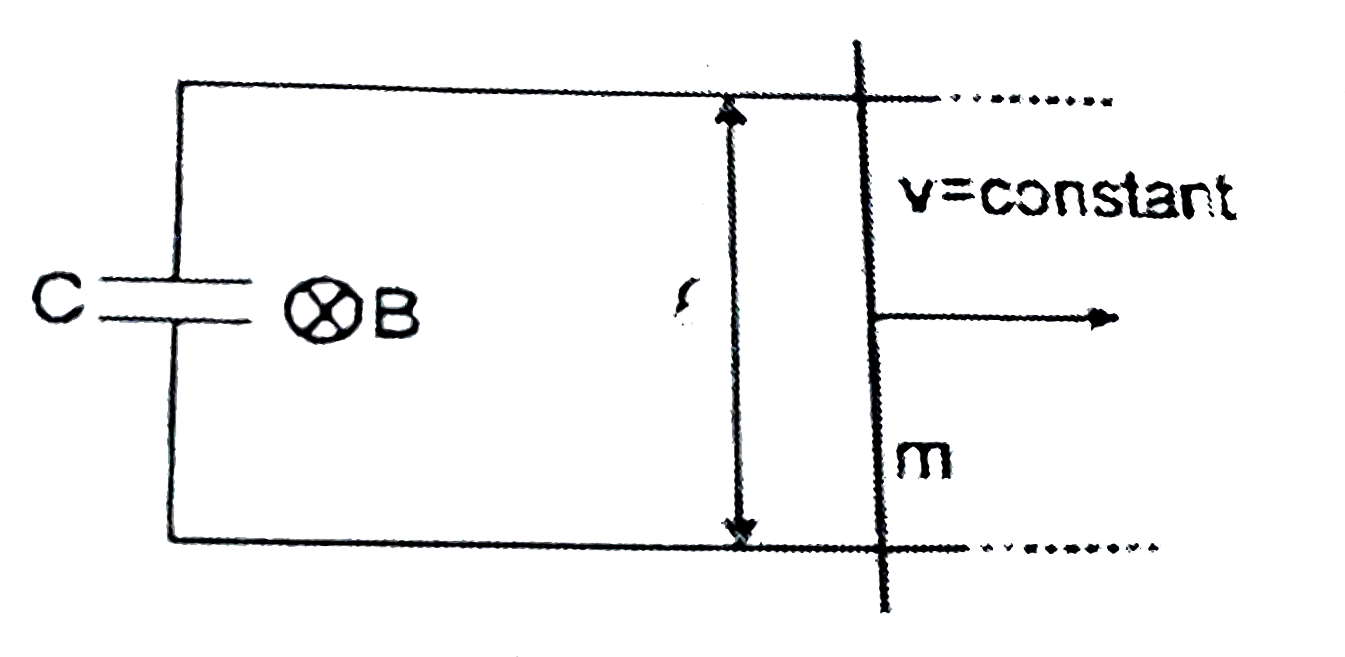
View SolutionIn the figure shown a conducting rod of length l, resistance R and mass m is moved with a constant velocity v. The magnitude field B varies with time t as B=5t, what t is time in second. At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged. the rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance. Find the current in the circuit as a function of time t.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conducting rod of mass m and length l is free to move without friction on two parallel long conducting rails, as shown below. There is a resistance R across the rails. In the entire space around, there is a uniform magnetic field B normal to the plane of the rod and rails. The rod is given an impulsive velocity v0-

Finally, the initial energy 12mv20AWill be converted fully into heat energy in the resistorBWill enable rod to continue to move with velocity v0 since the rails are frictionlessCWill be converted fully into magnetic energy due to induced currentDWill be converted into the work done against the magnetic field - Question 2 - Select One
Two ideal batteries of emfV1andV2 and three resistance R1R2andR3 are connected The current in resistance R2 would be zero if
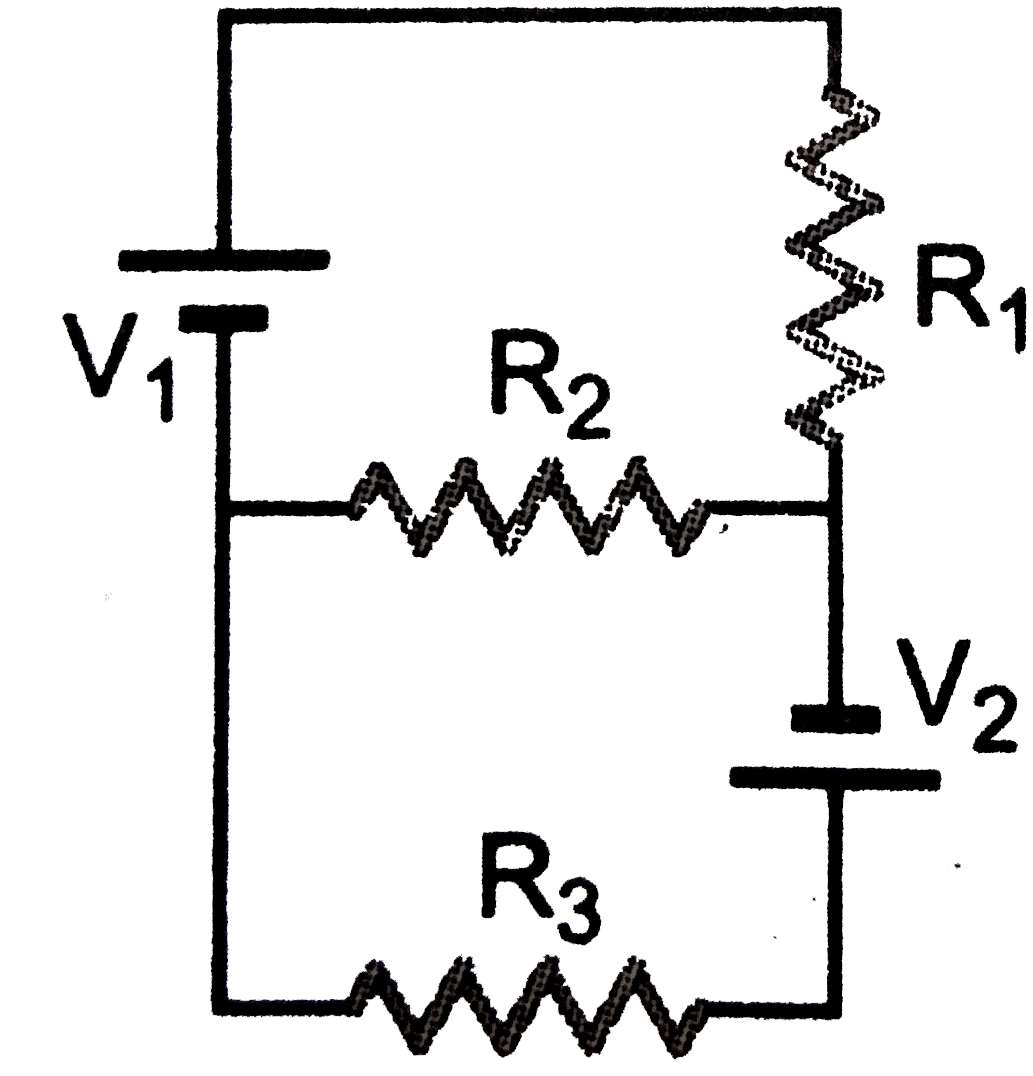 AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and2R1=R2=R3
AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and2R1=R2=R3 - Question 3 - Select One
A rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
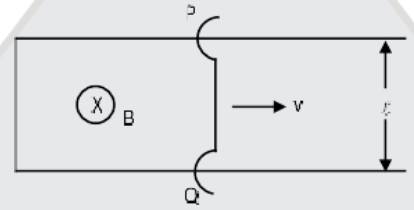 A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
Two parallel vertical metallic bars XX1 and YY1, of negligible resistance and separated by a length 'l', are as shown in Fig. The ends of the bars are joined by resistance R1 and R2. A uniform magnetic field of induction B exsits in space normal to the plane of the bars. A horizontal metallic rod PQ of mass m starts falling vertically, making contact with the bars. It is oberved that in the steady state the powers dissipated in the resistance R1 and R2 and the terminal velocity attained by the rod PQ.
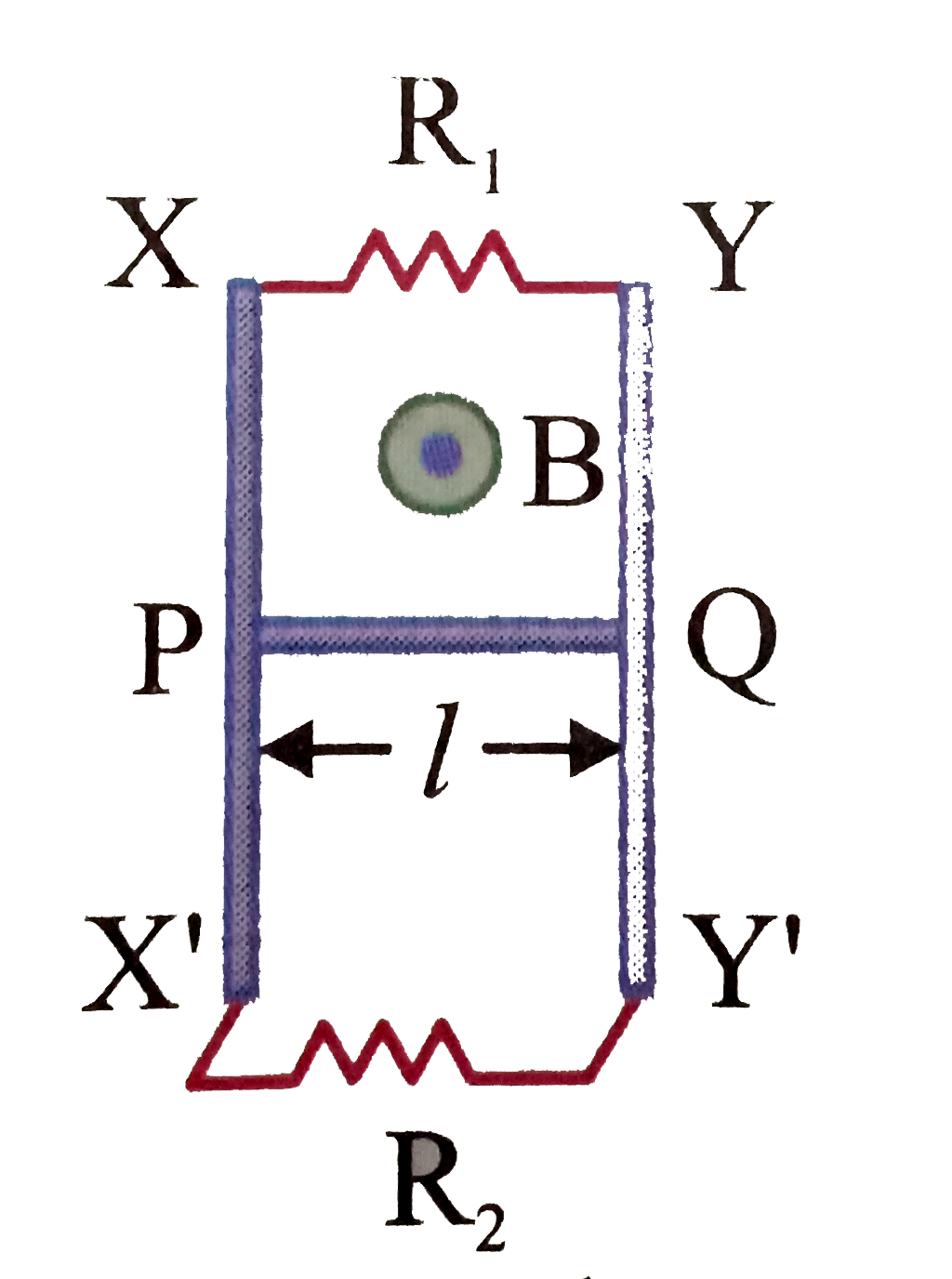 View Solution
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
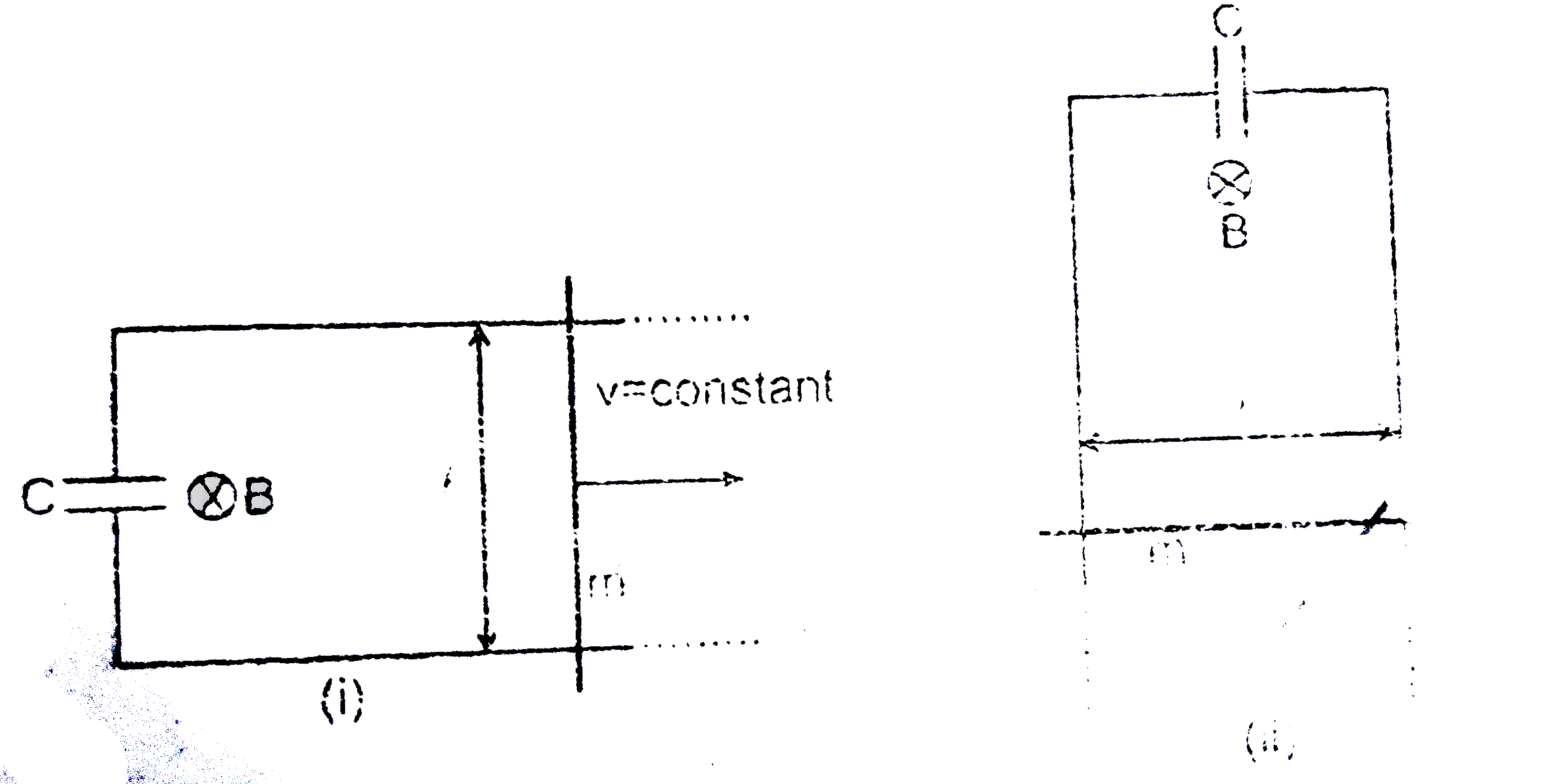 View Solution
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
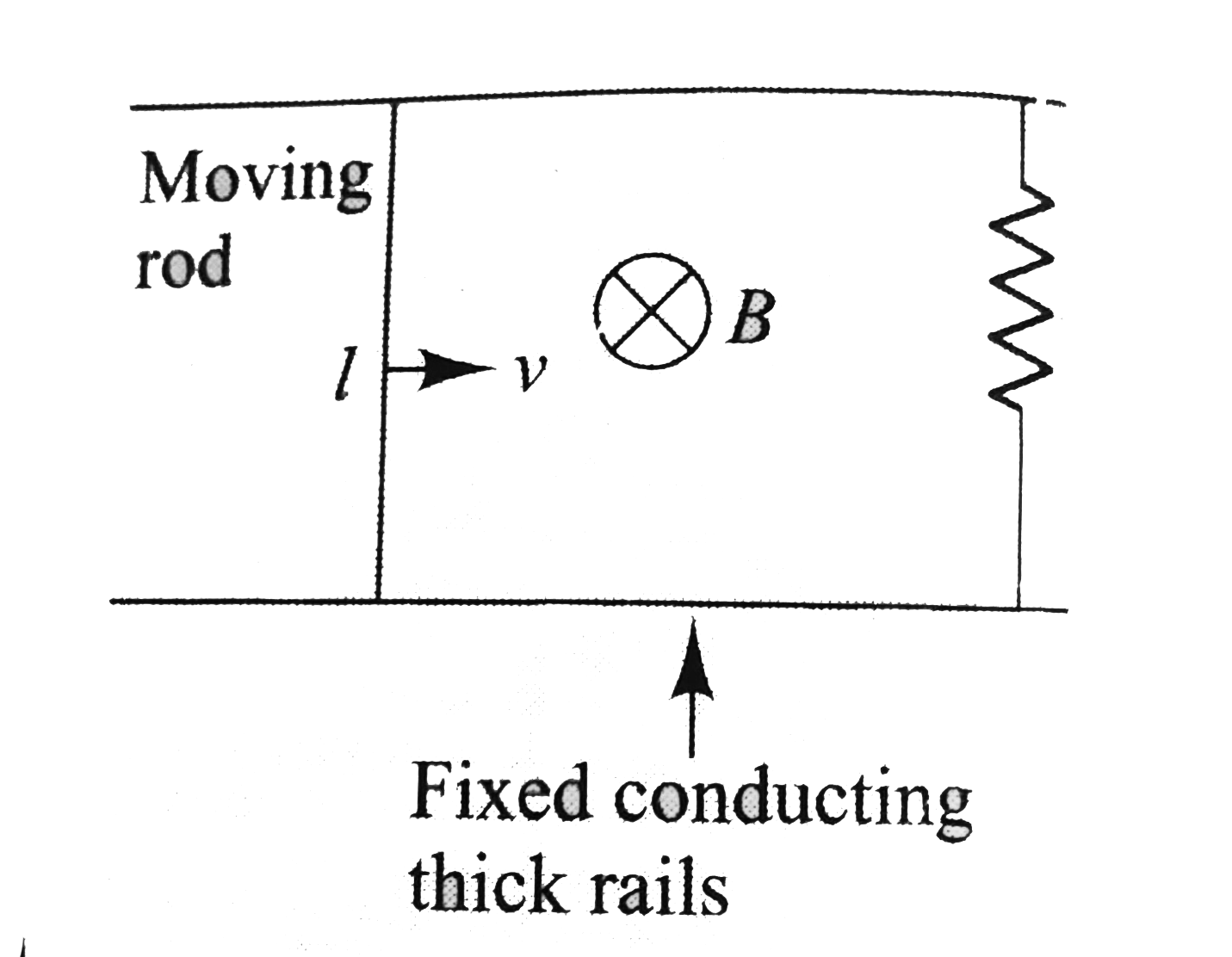 View Solution
View SolutionA rod of mass m and resistnce R sldes on frictionless and resistanceless rails a distance l a part thast innclude a source of emf E0 (see figure). The rod is initially at rest. Find the expression for the
a. Velocity of the rod v(t). b. current in the loop i(t).
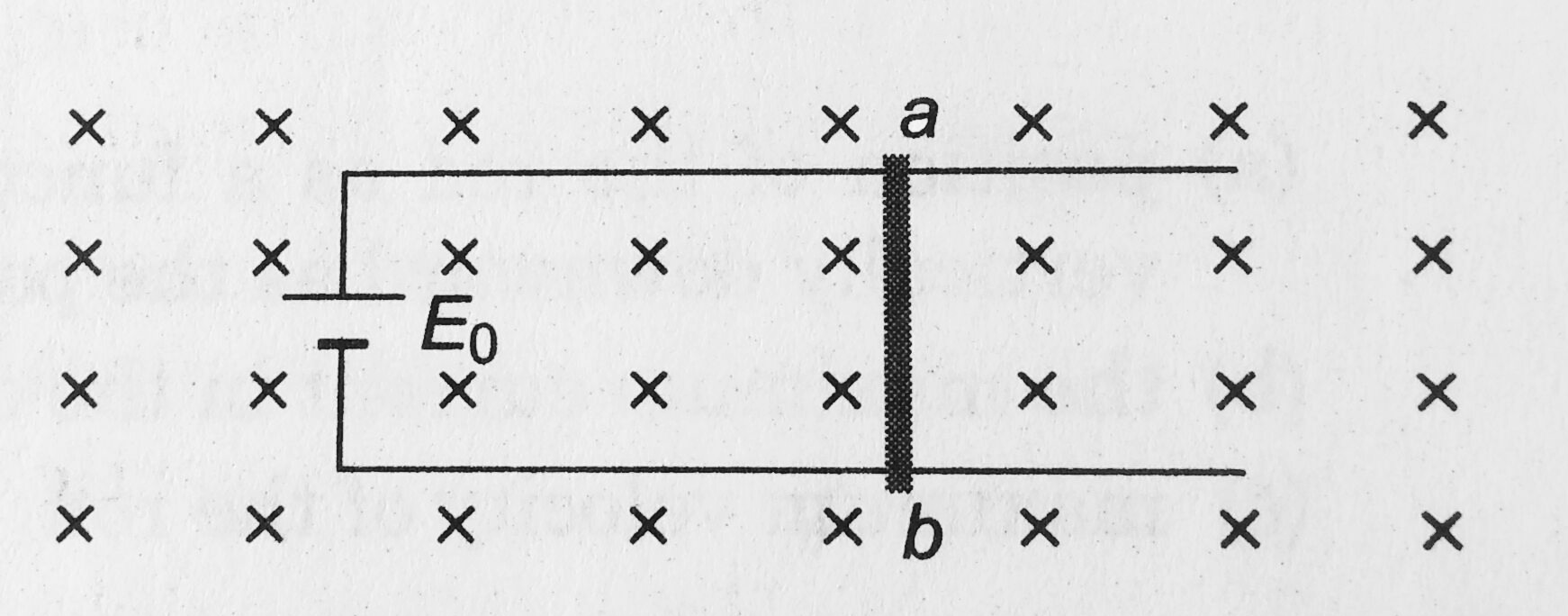 View Solution
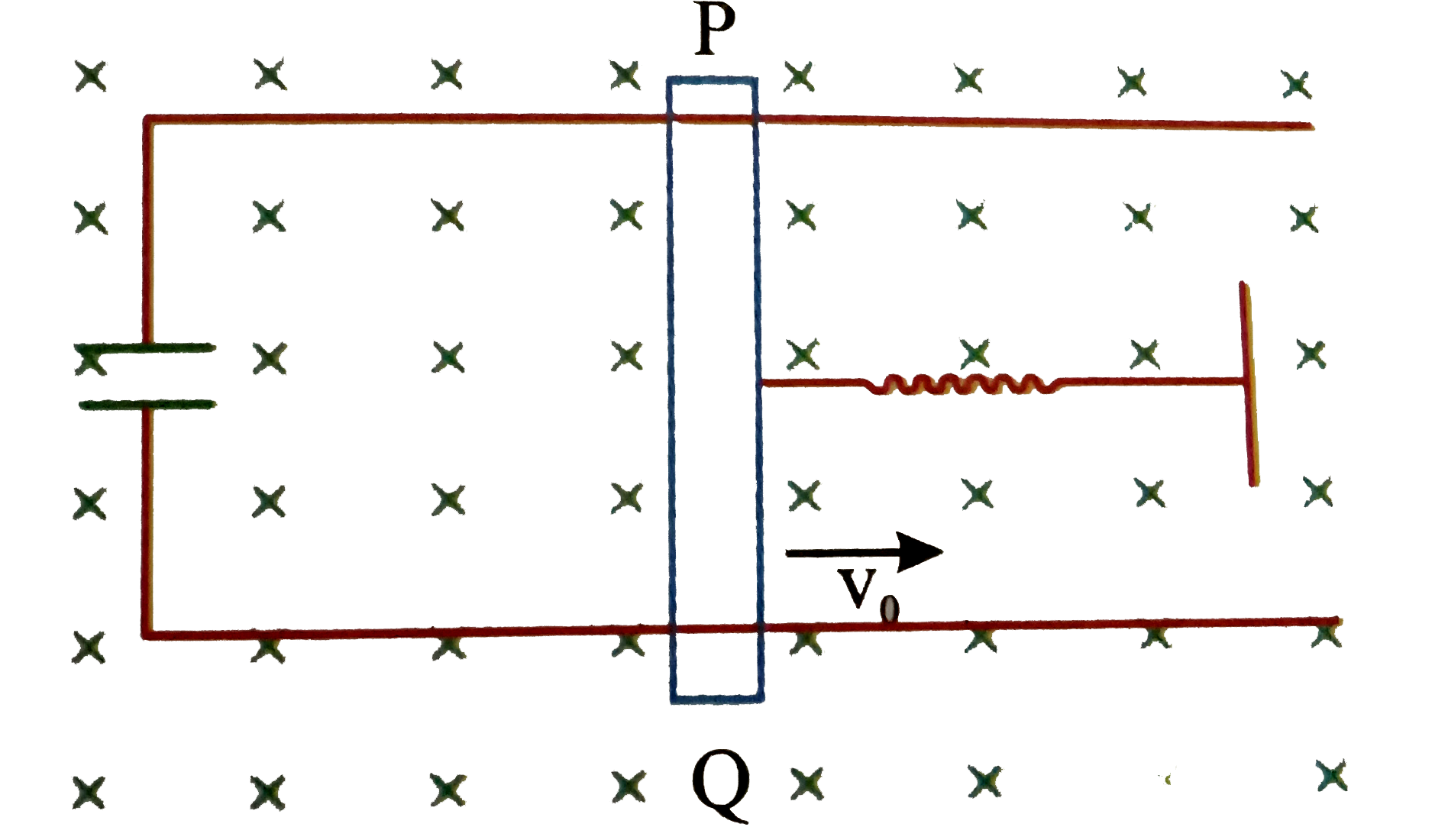
View SolutionA conducting rod PQ of mass m and length l is placed on two long parallel (smooth and conducting) rails connected to a capacitor as shown. The rod PQ is connected to a non conducting spring of spring constant k, which is initially in relaxed state. The entire arrangement is placed in a magnetic feild perpendicular to the plane of figure.
Neglect the resistance of the rails and rod.
Now, the rod is imparted a velocity v0 towards right, then acceleration of the rod as a function of its displacement x given by
 View Solution
View Solution

